前言

在这篇文章中主要看两种LR语法分析技术，相对于上一篇中SLR，本篇文章的两种LR技术对它进行了扩展，在输入中向前看一个符号。这两种技术分别是：

  • “规范LR”：也可以直接叫做”LR”方法，这个方法会使用很大的一个项集，称为LR(1)项集；
  • “向前看LR”：也可以直接叫做”LALR”方法，它基于LR(0)项集（比LR(1)项集状态要少很多）。很多情况下LALR是最合适的选择；

一、规范LR(1)

我们来看个情况，在SLR方法中，如果项集 包含项 ，如果当前输入符号 a 存在于FOLLOW(A)中。如果基于SLR来说，那么我们肯定会将 α 归约为A。然而在某些情况下，当状态 i 出现在栈顶时，栈中的可行前缀是 βα ，并且最右句型中 a 都不可能跟在 βA 之后，也就是说我们肯定不能简单就将 α 归约为 A 。

因此我们可以在项中新增一个分量，这个分量为一个终结符号。比如现在项可以表示为 ，其中 是一个产生式，而a是一个终结符号或者右端结束标记$。我们称这样的项为 LR(1)项 。其中的1指的是第二个分量的长度。

第二个分量称为 向前看符号 。

正式的说，LR(1)项对于可行前缀 γ 有效的条件是存在推导，其中：

  • 可行前缀为 xα；
  • 要么 a 是 w 的第一个符号，要么w为空串且a对于结束符；

构造LR(1)项集

LR(1)项集构造方法：一个增广文法G‘，在原来SLR的基础上对CLOSURE函数和GOTO函数进行改造。大致如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
SetOfItems CLOSURE(I) {
    repeat
        for(I中的每个项[A -> α·Bβ, a]) {
            for(G'中每个产生式B -> γ) { 
/// 解释一下，G’表示增广文法（它包含了文法的所有产生式）；B -> γ 表示在增广文法中当存在产生式头部为当前项点号右边的非终结符号时，进行下面的操作
                for(FIRST(βa)中每个终结符号b) {
                    将[B -> γ, b]项添加到集合I中；
                }
            }
        }
    until 不能向I中加入更多的项；
    return I;
}
SetOfItems GOTO(I,X) {
    将J初始化为空集；
    for (I中的每个项 [A -> α·Xβ, a])
/// 这里我解释一下，循环I中的每一个项，直到出现点号右边的符号和传入的参数符号X相同时进行后续操作
        将项[A -> αX·β, a]加入到集合J中; 
    return CLOSURE(J);
}
void items(G') {
    将C初始化为{CLOSURE}({[S' -> ·S, $]});
    repeat 
        for(C中每个项集I) {
            for(每个文法符号X) {
                if (GOTO(I,X)非空且不在C中)
                    将GOTO(I,X)加入C中；
            }
        }
    until 不再有新的项集加入到C中
}

下面的代码是我对上面的表示翻译了一下，看下面代码时可以对照上面的内容对应着看。而且对Item进行了更新，因为在LR(1)项集中Item需要一个向前看运算符：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
/*
struct Item {
int position; /// 点号所处位置
int id; /// 当前项在产生式集合中的编号
Symbol *forwardSymbol; /// 向前看符号
Item(){
    position = 0;
    id = 0;
    forwardSymbol = nullptr;
}
Item(int pos, int idt, Symbol *ptr):position(pos),id(idt),forwardSymbol(ptr){}
};
*/
SetOfItems<Item> LR_1::LRCollection::closure(SetOfItems<Item>& set) 
{
    for (SetOfItems<Item>::iterator itr = set.begin(); itr != set.end(); ++itr)
    {
        Item item = *itr;
        vector<Production> productions = grammer.productions;
        Production prod = productions[item.id];
        Symbol *dst_sym = prod.bodies[item.position];
        for (vector<Production>::iterator p_itr = productions.begin(); p_itr != productions.end(); ++p_itr)
        {
            int index = p_itr - productions.begin();
            if((p_itr->header).identifier() != dst_sym->identifier())
            {
                continue;
            } 
            Symbol *beta = prod.bodies[item.position + 1];
            vector<Symbol *>first = grammer.FIRST(beta);
            if (first.size() <= 0)
            {
                first = grammer.FIRST(item.forwardSymbol);
            }
            for (vector<Symbol *>::iterator s_itr = first.begin(); s_itr != first.end(); ++s_itr)
            {
                Item itm(0,index, *s_itr);
                set.push_back(itm); /// <------------------------ 自增长
            }
        }
    }
    return set;
}
SetOfItems<Item> LR_1::LRCollection::lr_goto(SetOfItems<Item>& set, Symbol *symbol, int *offset)
{
    SetOfItems<Item> temp;
    for (SetOfItems<Item>::iterator itr = set.begin(); itr != set.end(); ++itr)
    {
        Item item = *itr;
        Production prod = grammer.productions[item.id];
        Symbol *sym = prod.bodies[item.position];
        if (sym->identifier() != symbol->identifier())
        { /// 目标符号不符合
            continue;
        }
        int position = item.position + 1;
        if (position >= prod.bodies.size())
        { /// 异常
            continue;
        }
        
        Item result(item.id, item.position + 1, item.forwardSymbol);
        temp.push_back(result);
    }
    return closure(temp);
}
void LR_1::LRCollection::items()
{
    /// 1、将[S' -> .S, $]作为初始化加入到集合中
    SetOfItems<Item> set;
    Item it(0,0,const_cast<Symbol *>(Symbol::EndedSymbolPtr())); /// 产生式集合中第0个为增广表达式
    set.push_back(it);
    vector<SetOfItems<Item> > collection(1, set);
    using vector_type=vector<SetOfItems<Item>>;
    for(vector_type::iterator itr = collection.begin(); itr != collection.end(); ++itr)
    {
        vector <Symbol *> symbols = grammer.symbols;
        for (vector<Symbol *>::iterator s_itr = symbols.begin(); s_itr != symbols.end(); ++s_itr)
        {
            int offset = 0;
            SetOfItems<Item> items = lr_goto(*itr, *s_itr, &offset);
            int result = contain_set(items);
            if (result == -1)
            {
                collection.push_back(items);
                Item item = items[0];
                std::string key  = format("%d_%d_%d",item.id,item.position, item.forwardSymbol->identifier());
                item_map.insert(make_pair(key, offset));
            }
        }
    }
}

现在我们来看一个增广文法，我们使用上面的知识可以对这个增广文法构造出它对应的项集：

下图是对应的项集族：

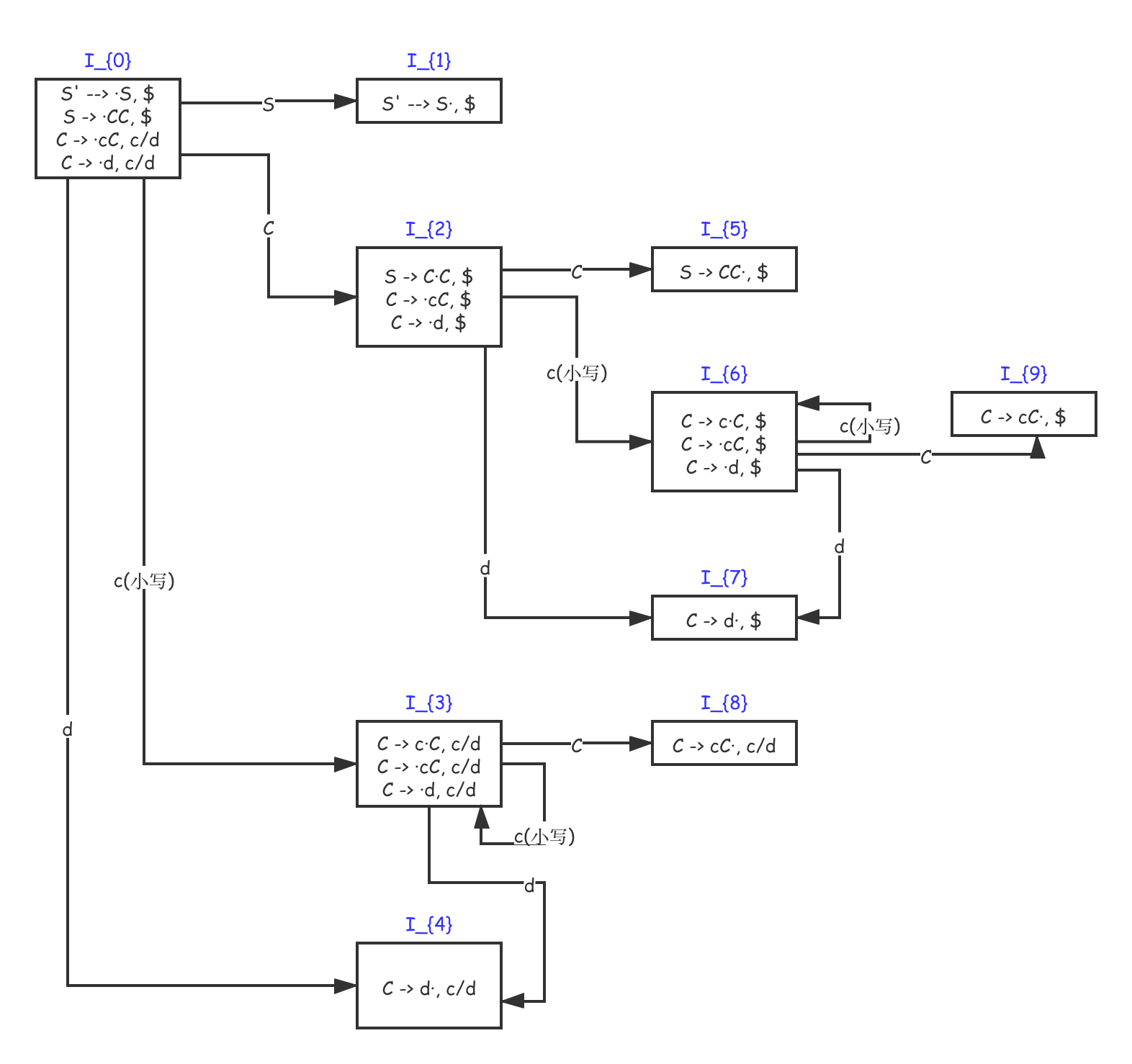
这个项集中的和上一篇文章中看到的项是不仅仅有了点号位置区分，还有向前看运算符的区分。

下面我们来看一下规范LR中ACTION函数的具体行为：

  • 1）、如果 在 中，并且 ，那么将 ACTION[i, a] 设置为“移入j”。这里 a 必须是一个终结符号；
  • 2）、如果 在 中且 （即当前产生式头部的非终结符，不是产生式集合中的增广文法的开始符号），那么将 ACTION[i, a] 设置为“归约A -> α”；
  • 3）、如果 在 中，那么将 ACTION[i, a] 设置为“接受”；
  • 4）、不满足上诉规则的，都设置为“报错”；

现在我们根据上面的四个规则，写出规范LR对应的ACTION函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
LR_Action* LR_1::LRCollection::action(SetOfItems<Item>& set, Symbol *symbol) 
{
    if (symbol->isTerminal() == false)
    {
        return nullptr;
    }
    LR_Action *action = set.actionForSymbol(symbol->identifier());
    if (action != nullptr)
    {
        return action;
    }
    vector<GrammarParser::Production> productions = grammer.productions;
    for (SetOfItems<Item>::iterator itr = set.begin; itr != set.end(); ++itr)
    {
        Item item = *itr;
        GrammarParser::Production prod = productions[item.id];
        if (item.position == prod.bodies.size()) /// 当前项的点号在最右边
        {
            if (item.id == 0 && symbol == GrammarParser::Symbol::EndedSymbolPtr())
            { /// 接受状态
                AcceptAction *action = new AcceptAction();
                return action;
            }
            
            if (item.forwardSymbol->identifier() == symbol->identifier)
            { /// 归约
                ReduceAction *redue = new ReduceAction(&prod);
                set.setActionForSymbol(symbol->identifier(), redue);
                return redue;
            }
            continue;
        }
        int offset = -1;
        SetOfItems result = lr_goto(set,symbol, &offset);
        if (result != set) /// 不同的两个状态，说明goto函数有效，此时应该做移入操作
        {
            action = new ShiftAction(offset);
            set.setActionForSymbol(symbol->identifier(), action);
            return action;
        }
    }
    ErrorAction *aciton = new ErrorAction();
    return action;
}

每个SLR(1)文法都是LR(1)文法。但是对于一个SLR(1)文法而言，规范LR(1)语法分析器的状态要比一个文法对应的SLR语法分析器的状态多。

普遍而言，同一个文法的规范LR语法分析器状态要比SLR语法分析器状态多；

二、LALR

现在来看最后一个语法分析器LALR语法分析器。在实践中，用这种方法得到的分析表比规范LR分析表 小很多，而且大部分常见的程序设计语言构造都可以方便地使用一个LALR文法表示。

现在我们再来看看下面这张图：

图中 中项的第一个分量是相同，不同的是向前看符号不同。现在我们将 替换为 （即的并集），这个项集中的元素为：。

原来在从经过b到达的转换，都转向为 。这个经过修改之后的语法分析器行为在本质上和原分析器一样。

在这里：

我们将项第一个分量称为 核心 。

因此上诉的步骤就是在寻找具有相同核心的LR(1)项集，并将这些 “项的集合” 合并为一个项集。关于项、项集、项集族的关系在上一篇文章中有进行说明。

比如就具有相同的核心 。

一般而言，一个核心就是当前正在处理文法的 LR(0) 项集，一个LR(1)文法可能产生多个具有相同核心的项集。

合并具有相同核心的状态不会产生出原有状态中没有出现的移入\归约冲突。因为移入动作仅有核心决定，不考虑向前看运算符。

其中提到的“移入动作仅有核心决定，不考虑向前看运算符”，我们可以看上一节ACTION函数具体行为的第一点。

简单地构造LALR分析器

构造语法分析器主要是从三个方面入手，分别是：确定项集，确定GOTO函数和确定ACTION函数。

  • 1）、我们从上面看出，我们可以先构造一个规范LR项集族，然后寻找具有相同核心的项集进行合并；

  • 2）、然后根据核心来确定GOTO函数的关系。如果J是一个或多个LR(1)项集的并集，即 ，它们能组成并集也就侧面反映了它们具有相同的核心。

    由于它们有相同的核心，那么的核心也是相同的。令K是所有和 具有相同核心项集的并集，那么 GOTO(J,X) = K 。

  • 3）、关于ACTION函数的逻辑和实现规范LR的类似的（移入、归约、接受）；

显然，这并不是高效的构造LALR语法分析器的方法。就比如在学习正则表达式转换为确定的有穷自动机（DFA）时，我们最初使用的正则表达式转换为NFA，然后通过子集构造法得到DFA。经过探索之后可以直接使用nullable、firstpos、lastpos以及followpos将正则表达式转换为DFA。

同样的，我们也可以用更加高效的方法来构造LALR语法分析表。

⚠️⚠️⚠️ 高效构造LALR语法分析表

我们可以对上面的方法进行修改，使得我们在创建LALR(1)语法分析表的过程中不需要构造出完整的规范LR(1)项集族。

在介绍具体的思想之前，我先解释一下“内核项”。它在上一篇文章中提到，总体来说就是 点号不在最左边，但是增广文法的第一个产生式除外 。下面是构造高效LALR语法分析表的大致思路：

  • 1）、首先，我们可以只使用内核项来表示任意的LR(0)和LR(1)项集；

  • 2）、使用“传播和自生成”的过程来生成向前看符号，根据对应的LR(0)项内核生成LR(1)项内核。

    这里我稍微多说一句，“传播和自生成”都是针对向前看符号而言的，“传播”是指我们从上一个项集对应的向前看符号传到下一个项集，作为对应项的向前看运算符。“自生成”则是指的根据GOTO函数和CLOSURE函数生成的向前看符号，具体的生成规则会在下面讲解；

  • 3）、当有了内核之后，就可以使用CLOSURE函数对各个内核求其余项，最后生成语法分析表；

现在我们需要给LR(0)内核加上正确地向前看符号，创建出正确地LALR(1)内核。现在来看一个内核项 ，以及存在对应产生式 ，我们先来看CLOSURE和GOTO：

其CLOSURE函数结果为：

其中GOTO函数的结果为：GOTO(I, B) = ;

这儿我为什么要求这两个函数的值呢？因为它们和“传播和自生成”关系密切，对于GOTO函数之后得到的项集而言：

  • 如果FIRST(βa) == a 也就是说明FISRT(β)为空，也就是说我们不能在GOTO(I, θ)中自己生成一个向前看符号，因此我们将原来内核项的向前看符号 传播 到新的内核项；
  • 如果FIRST(βa) != a 也就是说明FISRT(β)不为空，那么我们就可以通过FISRT(β) 自生成 一个向前看符号；

有了上面的基础之后，我相信下面这段话应该就可以看懂了：

令#为一个不在当前文法中的符号，令 为内核LR(0)项。对于每个 X(文法符号) 计算 。 对于J中的每个内核项，我们检查它的向前看符号集合：

1、如果#是它的向前看符号，那么向前看符号就是从 传播到这个项的；

2、除此之外其他的向前看符号都是自发生成的；

向前看符号 $ (结束符号) 对于初始项集中的项 而言是自发生成的

伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
for (K中的每个项 A -> α·β)
{
    J = CLOSURE({[A -> α·β, #]});
    if ([B -> γ·Xδ, a]在J中，并且a不等于#)
    {
        那么GOTO(I,X)中的项B -> γX·δ向前看符号a是自生成的；
    }
    if ([B -> γ·Xδ, a]在J中)
    {
        那么向前看符号从I中的项A -> α·β传播到了B -> γX·δ上；
    }
}

那么到这儿应该就在想，这个传播的最初源头在哪儿呢？很明显这个源头就是增广文法的初始项集。

这块儿主要是理解传播和自生成向前看运算符。

到这儿我们也把规范LR和LALR大致了解了一下，在实际的运用中主要还是使用LALR的语法分析。其原因是它可以通过向前看一个符号来解决移入归约冲突，还有就是可以减少语法分析过程中出现的状态数量。

题外话，后面一段时间我可能不会更新编译原理相关的文章了，回归时间待定了。