前言
自顶向下语法分析可以被看作是为输入串构造语法分析树的问题,它从语法分析的根节点开始,按照深度优先的规则创建这棵语法分析树的各个结点,自顶向下语法分析也可以被看作寻找输入串最左推导的过程。
本文的行文以下面的顺序展开:
1)、首先是以一个自顶向下语法分析的例子,为自顶向下语法分析有个大致的认识;
2)、其次我们就需要深入地了解自顶向下语法分析中使用到的“ 递归下降语法分析”;
3)、但递归下降的语法分析存在一个很大的弊端就是有回溯的可能性,为了减少回溯的次数,因此我们需要向前看多个字符。 LL(k) ,其中k表示向前看的字符数;
4)、为了能够更加准确地知道向前看字符,我们需要构造“ 预测分析表 ”,而 FIRST 和 FOLLOW 集合是构造预测分析表必不可少的部分;
好吧,那我们先来看一个自顶向下的语法分析例子。
一、自顶向下语法分析示例
我们消除了左递归之后的文法(关于消除左递归可在上一篇文章中查看):
对于输入串 id + id*id 语法分析树推导序列如下图所示:
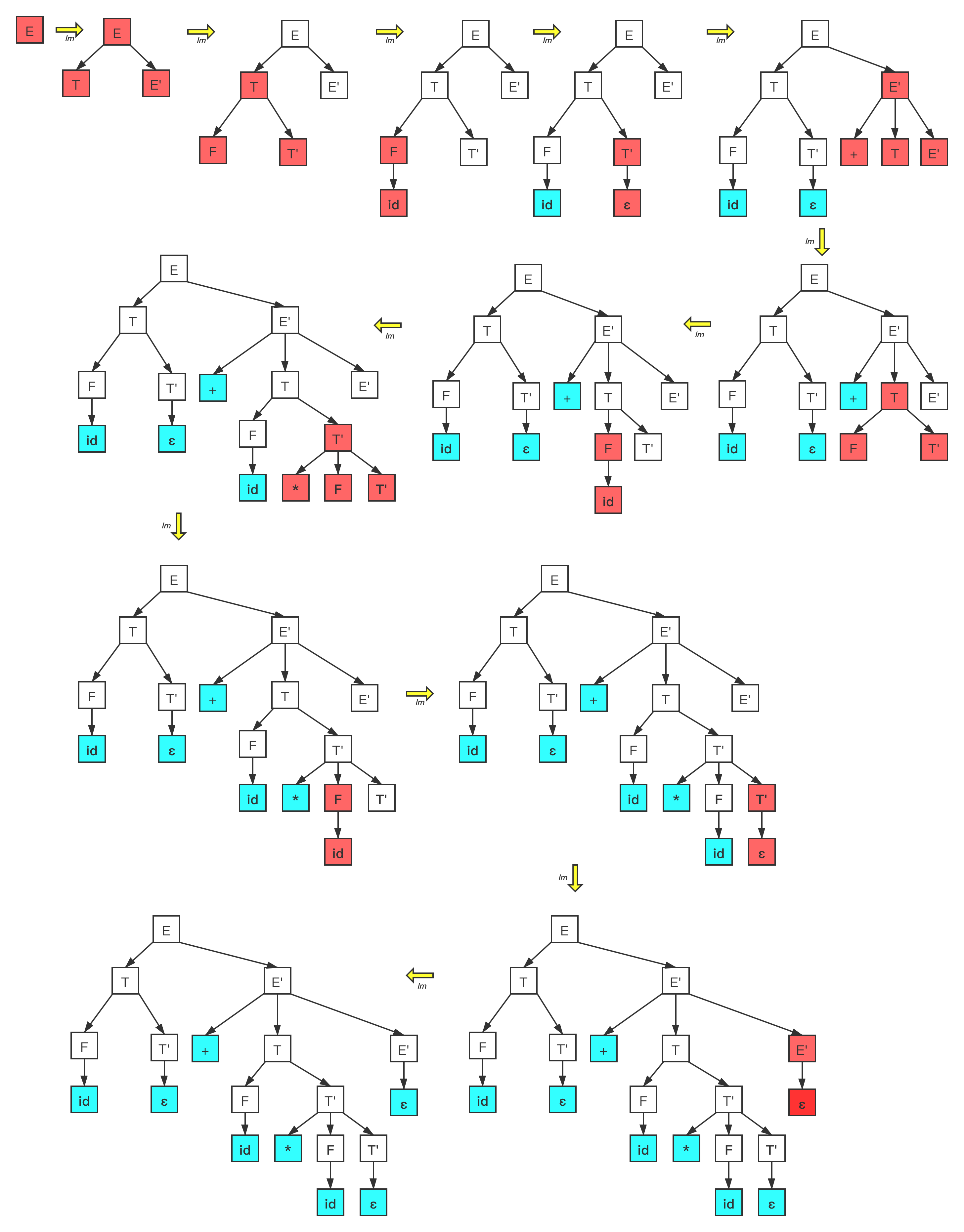
这里使用的最左推导,每次都是寻找当前语法分析树中最左边的非终结符进行推导操作。在自顶向下的分析过程中,对于同一非终结符号的选择指定产生式成为了关键问题,比如对于非终结符F来说,它存在两个产生式 和 ,如果我们选择错误之后,则难免需要进行回溯,并替换为另一个正确地产生式。这种分析方式就是我们首先要学习的 递归下降语法分析 。
但我们可以使用预测分析技术来避免回溯的发生,它通过向前看固定多个符号来选择正确地产生式。比如我们向前看 k 个符号,那么这类文法为 LL(k) 文法。而我们后续要学习的LL(1)文法,就是该文法的特例。即我们向前看1个符号。
递归下降的语法分析
一个递归下降语法分析程序由一组过程(也可以理解为C语言里面的函数)组成,每个非终结符号有一个对应的过程。比如:
1 2 3
| void expr() {...} void statement() {...} void S() {...}
|
程序的执行从开始符号对应的过程开始,如果这个过程完整地扫描了整个输入串,它就停止执行并宣布语法分析成功完成。
下面是一段伪代码:
1 2 3 4 5 6 7 8 9 10 11 12 13
| void X1() {...} void X2() {...} ... void Xk() {...} void A() { 选择一个A产生式:A -> X1X2X3... Xk; /// 需要注意的是这里X1, X2, X3, ... Xk组成的一个符号串,并不是非终结符号A的多个产生式 for(i = 1 to k) { if (Xi 是一个非终结符号) { 调用Xi(); } else if (Xi等于当前的输入符号a) { 读取下一个输入符号; } else { 发生错误; } } }
|
上面的Xi有可能就是非终结符号A自身,因此可能会形成递归调用的场景。通用的递归下降分析技术可能需要回溯,也就是说我们可能需要重复扫描输入。要支持回溯的话,那我们就需要修改上面的代码:
1)、首先需要按照非终结符号产生式的顺序逐个尝试各个产生式;
2)、然后需要一个局部指针变量来保存当前进行匹配的符号;
3)、如果发生当前既不是非终结符号,又不等于当前的输入符号时。我们需要将输入符号回溯到局部指针变量指向的符号;
4)、如果再也没有当前非终结符号产生式可尝试时,我们才认为发生了错误;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
| void X1() {...} void X2() {...} ... void Xk() {...} char *input_char; /// 输入字符 void A() { 非终结符号A的产生式集合:{ A->X1X2X3... Xk, A->Y1Y2Y3... Yk, A->Z1Z2Z3... Zk ... } for (选择一个A产生式:A -> X1X2X3... Xk) { /// -----> 1 char *pivot = &a; /// -----> 2 for(i = 1 to k) { if (Xi 是一个非终结符号) { 调用Xi(); } else if (Xi等于当前的输入符号*input_char) { 读取下一个输入符号; input_char++; } else { input_char = pivot; /// -----> 3 break; } /// 继续读取下一个产生式 } } if (*input_char == *pivot) { 发生了错误; /// -----> 4 } }
|
Ⅰ、具体实例
下面我们来看一个具体的例子,对于文法:
对于输入串 w = cad,其递归下降的语法分析过程为:
- 1、对于开始符号 ,并且此时的输入指针为
c,此时我们展开开始符号S
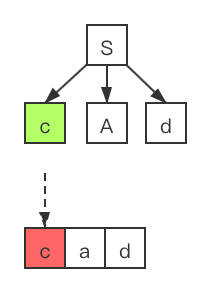
- 2、从输入指针指向的输入符号
c 和当前开始符号S展开的语法分析树最左边的叶子结点c相匹配,此时我们将指针移动到 a,并且考虑当前语法分析树的非终结符号A(从左到右扫描符号)。
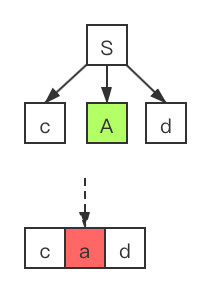
- 3、我们使用产生式 进行展开。很明显第二个输入符号
a 匹配成功。
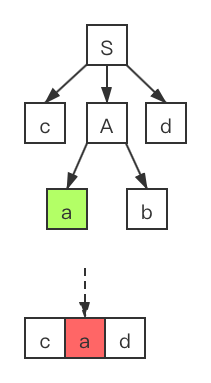
- 4、现在我们将输入指针移动到
d ,并且把语法分析树的当前结点移动到结点 b 。很明显可以看出来 d 和 b 并不匹配。
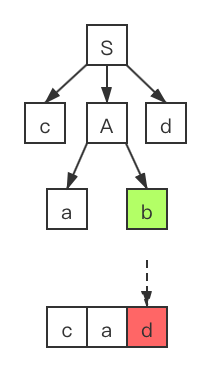
- 5、此时我们需要查看对于非终结符号A,是否存在尚未尝试过的产生式。在回到A时,我们需要将输入指针回退到上一个位置处,并且使用产生式 进行推导:
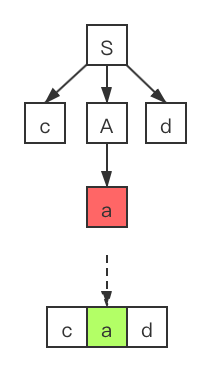
叶子结点 a 和当前输入指针指向的输入符号成功匹配。同样的移动输入指针到 d ,并且将目光移向语法分析树最右边的叶子结点处,它们同样是匹配的。因此上图中的语法分析树就是通过递归下降得到的结果。
一个左递归的文法会使得它的递归下降语法分析器进入一个无限循环。
由于回溯不是很高效,我们可以使用动态规划算法,构造基于表格的的方法。我会在单独的一篇文章来介绍一下动态规划。
二、🍺🍺🍺 FIRST和FOLLOW集合(终结符号)
关于FIRST集合和FOLLOW集合一定要弄懂,因为这是在后续进行预测分析时必备的技能。在自顶向下的语法分析过程中,FIRST和FOLLOW使得我们可以根据下一个输入符号来选择应用哪个产生式。
Ⅰ、FIRST
FIRST(α) :从 α 可以推导出一个串集合,而FIRST为这些串首个符号组成的集合;
如果 (箭头上方的星号 * 表示 α 可以通过多个步骤之后得到 ε ),那么 ε 就在 FIRST(α) 中。又或者存在推导
那么终结符号 c 也在 FIRST(α) 中。
计算文法符号X的FIRST(X)时,不断应用下面的规则,直到再没有新的 终结符号或者ε 可以被加入到任何FIRST集合中为止:
- 1)、如果X是终结符号,那么FIRST(X) = X;
2)、如果X是一个非终结符号,且存在产生式 (其中k>1):
如果终结符号 a 在 中的必要条件是 中包含有 ε 符号;
比如 中所有符号一定都在 中,如果 不能推导出 ε,那么我们就没有必要再向 加入任何符号。但是如果 能推导出 ε,那么我们就需要查看其后非终结符号的推导情况了。
简单来说就是,对于文法中非终结符号的产生式而言,观察其产生式体能够推导出终结符号的集合。
- 3)、如果 是一个产生式,那么 ε 加入到 FIRST(X) 中;
也就是说:
对于FIRST(α)我们看产生式头可以推导得到的产生式体中的首个符号集合,即计算FIRST时非终结符号处于产生式的头部。
下面是FIRST集合求解的代码(靠着自己理解编写,难免存在问题,如有问题麻烦指出):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
| vector<Symbol *> GrammarParser::ContextFreeGrammar::FIRST(Symbol *sym) { /// 视角总是把当前符号当做产生式的头部 vector<Symbol *>firsts; /// 1、如果是一个终结符号,那么FIRST返回它自身 if (sym->isTerminal()) { firsts.push_back(sym); return firsts; } /// 2、如果是一个非终结符号,并且是一个产生式 for (vector<Production>::iterator itr = this->productions.begin(); itr != this->productions.end(); ++itr) { Nonterminal header = itr->header; /// <--------- 产生式头部 if (header.identifier() != sym->identifier()) { continue; } vector<Symbol *>bodies = itr->bodies; for (vector<Symbol *>::iterator s_itr = bodies.begin(); s_itr != bodies.end(); ++s_itr) { if (*s_itr == Symbol::EmptySymbolPtr()) { /// 3、如果是一个推出空串的产生式 firsts.push_back(*s_itr); continue; } vector<Symbol *>temp = FIRST(*s_itr); firsts.insert(firsts.end(),temp.begin(),temp.end()); /// 递归查看当前符号的FIRST集合情况 } } return firsts; }
|
Ⅱ、FOLLOW
FOLLOW(A):定义为在某些句型中,紧跟在非终结符号A右边的终结符号集合。
比如对于句型 ,终结符号 a 就在 FOLLOW(A) 中。如果非终结符号A是某些句型的最右符号,那么特殊的 “结束标记” $ 也在FOLLOW(A)中。
和FIRST集合类似,计算所有非终结符号A的FOLLOW(A)集合时,不断应用下面的规则,直到再没有 新的终结符号 可以被加入到任意FOLLOW集合中为止:
- 1)、将 $ 放到FOLLOW(S)中,其中S是开始符号,而 $ 是输入右端的结束标记;
- 2)、如果存在一个产生式 ,那么FIRST(β)中除了ε之外的所有符号都在FOLLOW(B)中。即这块儿需要查看符号串β的推导;
- 3)、如果存在一个产生式 ,那么FOLLOW(A)中所有的符号同时也都在FOLLOW(B)中;
也就是说:
计算FOLLOW时非终结符号位于产生式体中,查看当前产生式体中(或者叫句型的右边部分)非终结符号紧挨着的 终结符号 集合。
下面是FOLLOW集合的请求代码(和上面相同,同样可能存在问题):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81
| vector<Symbol *> GrammarParser::ContextFreeGrammar::FOLLOW(Symbol *sym) { /// 视角总是将当前符号放在产生式体中 vector <Symbol *> follows; /// 1、如果当前符号时开始符号,那么将结束标记加入到follows中 if (sym->identifier() == productions[0].header.identifier()) { Symbol *end = const_cast<Symbol *>(Symbol::EndedSymbolPtr()); follows.push_back(end); return follows; } if (sym->isTerminal()) { return follows; } /// 判断当前迭代器是否是body中的最后一个符号, auto expr_last = [&follows,this](vector<Symbol *>::iterator current, vector<Symbol *>::iterator begin, size_t count, Symbol *header_ptr) -> bool { size_t idx = current - begin; bool result = false; if (idx == count - 1) /// 当前符号处于产生式体的末尾 { /// 如果存在一个产生式 A --> aB,那么FOLOOW(A)中所有符号都在FOLLOW(B)中 vector<Symbol *> temp = FOLLOW(header_ptr); follows.insert(follows.end(), temp.begin(), temp.end()); result = true; } return false; }; /// 2、如果存在一个产生式 A --> aBb,那么FIRST(b)中除了空串以外,所有符号都在FOLLOW(B)中 for (vector<Production>::iterator itr = this->productions.begin(); itr != this->productions.end(); ++itr) { Nonterminal header = itr->header; Symbol *header_ptr = &header; vector<Symbol *>bodies = itr->bodies; size_t count = bodies.size(); vector<Symbol *>::iterator sym_itr = bodies.end(); /// 求解当前FOLLOW集合的符号指针; for (vector<Symbol *>::iterator s_itr = bodies.begin(); s_itr != bodies.end(); ++s_itr) { if (sym_itr != bodies.end()) { /// 第2种情况求解 size_t first_index = s_itr - sym_itr; if (first_index <= 0) { continue; } vector<Symbol *> firsts = FIRST(*s_itr); for (vector<Symbol *>::iterator first_itr = firsts.begin(); first_itr != firsts.end(); ++first_itr) { if (*first_itr == Symbol::EmptySymbolPtr()) { /// 3、如果存在一个产生式 A --> aB,或者产生式 A -->aBb(FIRST(b)包含空串),那么FOLOOW(A)中所有符号都在FOLLOW(B)中 bool result = expr_last(s_itr, bodies.begin(), count, header_ptr); size_t idx = s_itr - bodies.begin(); if (result) { sym_itr = bodies.end(); } break; } follows.push_back(*first_itr); sym_itr = bodies.end(); } } if (sym->identifier() != (*s_itr)->identifier()) { continue; } /// 3、如果存在一个产生式 A --> aB,或者产生式 A -->aBb(FIRST(b)包含空串),那么FOLOOW(A)中所有符号都在FOLLOW(B)中 bool result = expr_last(s_itr, bodies.begin(), count, header_ptr); if (result) { break; } sym_itr = s_itr; continue; } } return follows; }
|
Ⅲ、示例
我们对下面文法来求解FIRST和FOLLOW集合:
首先我们以非终结符号出现的顺序,将它们按照顺序排列起来(有点像消除左递归时,我们创建的非终结符号集合):
1)、 非终结符号E :
FIRST(E) = { ( , id },其推导过程为: ;
FOLLOW(E) = { ), $ }。从产生式 我们可以得到一个终结符号。而且从求FOLLOW的第一点可知,对于开始符号,我们需要将$添加进去。
2)、 非终结符号E’:
FIRST(E’) = { +, ε },其推导过程为:。
FOLLOW(E’) = { ), $ },这是因为产生式 可知,FOLLOW(E)和FOLLOW(E’)是完全等价的。
3)、 非终结符号T:
FIRST(T) = { ( , id },其推导过程为:
FOLLOW(T)的计算从上述的文法中可以看出,非终结符号T出现在产生式体中的有 ,也就是在其后面的均为非终结符号E’。因此FOLLOW(T)包含FIRST(E’);
由于E’可以推导出空串ε,而且根据产生式 。我们可以知道FOLLOW(T)同样等于FOLLOW(E)。因此求出上面两个的并集为:
FOLLOW(T) = { +, ), $ }。
4)、 非终结符号T‘:
FIRST(T’) = { , $ },其推导过程为:$$ T’\rightarrow FT’$$;
FOLLOW(T’) = { +, ), $ }。这是因为根据产生式 可知,FOLLOW(T’)和FOLLOW(T)是相同的;
5)、 非终结符号F:
FIRST(F) = { (, id },其推导过程为 ;
FOLLOW(F)的计算和非终结符号T是类似的,首先我们根据产生式 可知,非终结符号F其后紧跟着非终结符号T’,因此FOLLOW(F)则包含了FIRST(T’);
而且我们从产生式 可知,T’可以推导出空串ε,因此FOLLOW(F)也包含有FOLLOW(T);
因此最终的结论为:FOLLOW(F) = { *, +, ), $ }
如果这块儿存在无法理解的部分,可以对照例子,返回查看FIRST和FOLLOW的计算方式。
三、🍭🍭🍭LL(1)文法
LL(1)中的第一个“L”表示从左向右扫描输入,第二个“L”表示产生最左推导,而“1”则表示在每一步中只需要向前看一个输入符号来决定语法分析动作。我们利用LL(1)的文法,可以构造出不需要回溯的递归下降语法分析器(即预测分析器)。
左递归文法和二义性文法都不可能是LL(1)的
对于任意两个不同的产生式:,只有满足下面条件时,它们才是LL(1)文法:
1)、不存在终结符号a,使得 α 和 β 都能够推导出以 a 开头的串;
意思也就是说,FIRST(α) 和 FIRST(β) 是不相交的集合。
2)、 α和β中最多只有一个可以推导出空串;
当然这里一样的,FIRST(α) 和 FIRST(β) 是不相交的集合。如果出现了相交的集合,那么交集就是 ε 集。
3)、如果 ,那么 α 不能推导出任何以 FOLLOW(A) 中某个终结符号开头的串。类似的,对于 α 也一样;
这里我仔细的说一下,如果要推导出以FOLLOW(A)中某个终结符号开头的串,那也就是说 FIRST(α) 和 FOLLOW(A) 要存在交集。对于推导 而言,我们从第二点可以知道,那么此时 α 不能推导出 ε。这样看来要 FIRST(α) 和 FOLLOW(A) 存在交集,那是不可能发生的。
👏👏👏构建预测分析表
我们构造一个预测分析表 M 。该表是一个二维数组,其中第一列为文法中出现的各个非终结符号;其中第一行为文法中出现的终结符号。
NT:非终结符号
t:终结符号
| NT\t |
+ |
* |
( |
) |
id |
$ |
| E |
. |
|
|
|
|
|
| E’ |
|
. |
|
|
|
|
| T |
|
|
. |
|
|
|
| T’ |
|
|
|
. |
|
|
| F |
|
|
|
|
. |
对于文法G的每个产生式 ,处理如下:
1、对于FIRST(α)中每个终结符号a,将 加入到 M[A,a] 中。首先查看该产生式的FIRST集合,找到该集合中存在的所有终结符号a、b、c…
如果FIRST(α)不存在ε空串,那么对应非终结符号构造结束,寻找下一个产生式。
2、如果FIRST(α)中存在ε空串:
1)、对于FOLLOW(A)中每个终结符号b,将 加入到 M[A,b] 中;
2)、如果$在FOLLOW(A)中,将 加入到 M[A,$]中;
通俗一点来说就是,先看FIRST集合,如果FIRST集合里面包含了空串,然后再看对应的FOLLOW集合
简单一点来说就是,先查看对应产生式的FIRST集合,如果FIRST集无法推导出空串ε,那么该产生式结束,寻找下一个产生式;如果当前产生式FIRST可以推导出空串,那么求该非终结符号对应的FOLLOW集合和结束标记$。
同样的,我们还是以文法
举例:
下面使用的到FIRST集合FOLLOW集合的结果,是上一节里面求得的各个非终结符号的结果。具体可以对照上面内容一起看。
1)、对于非终结符号E而言,FIRST(E) = { ( , id },因此我们将产生式 填入到对应的格子里面:
2)、对于非终结符号E’而言,FIRST(E’) = { +, ε }。由可知FIRST(E’)可以推导出空串ε,因此我们需要获取FOLLOW(E’),得到 FOLLOW(E’) = { ), $ }。填写对应的格子如下:
3)、对于非终结符号T而言,FIRST(T) = { ( , id },可知其不能推导出空串。因此我们只需要填写FIRST集合里面对应表格即可:
4)、对于非终结符号T’而言,它和E‘有点相似之处。即我们从FIRST(T’) = { *, $ } 可知,其可以推导出空串。同样的我们需要查看 FOLLOW(T’) = { +, ), $ }
5)、对于非终结符号F而言,其FIRST(F) = { ( , id }
将上面的表格汇总之后就得到了我们最终的预测分析表:
| NT\t |
+ |
* |
( |
) |
id |
$ |
| E |
|
|
|
|
|
|
| E’ |
|
|
|
|
|
|
| T |
|
|
|
|
|
|
| T’ |
|
|
|
|
|
|
| F |
|
|
|
|
|
下面的代码是对LL(1)文法的语法预测分析表的一个伪代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86
| class ll_prediction_analysis_table { private: ContextFreeGrammar grammar; map<int,int> row_map; /// key: symbol id, value: table row index map<int,int> col_map; /// key: symbol id, value: table col index vector < vector<int> > table; private: void extract_symbol() { /// 从文法的各个产生式中分离出终结符和非终结符 int terminal_index = 0; for (vector<Production>::iterator itr = grammar.productions.begin(); itr != grammar.productions.end(); ++itr) { int index = itr - grammar.productions.begin(); vector<Symbol *> bodies = itr->bodies; for (vector<Symbol *>::iterator body_itr = bodies.begin(); body_itr != bodies.end(); ++body_itr) { if ((*body_itr)->isTerminal()) { col_map.insert((*body_itr)->identifier(), terminal_index); ++terminal_index; } } row_map.insert((itr->header).identifier(),index); } /// 添加结束符 int ended_key = (const_cast<Symbol *>(Symbol::EndedSymbolPtr()))->identifier(); col_map.insert(ended_key,terminal_index); vector <int> inner(col_map.size(),-1); vector <vector<int> >tb(row_map.size(), inner); table = tb; } void create_table() { /// 这里我默认是对应产生式有对应的LL(1)文法,也就是说表内每一项只包含一个产生式,不会包含多重定义的项。 auto map_itr = row_map.cbegin(); while (map_itr != row_map.cend()) { int table_row_index = map_itr->second; int key = map_itr->first; } for (vector<Production>::iterator itr = grammar.productions.begin(); itr != grammar.productions.end(); ++itr) { int index = itr-grammar.productions.begin(); Nonterminal header = itr->header; int row_index = col_map[header.identifier()]; /// 1.对于FIRST中每个终结符号a,将产生式 A --> α 加入到 table[A][a] 中 vector<Symbol *> first = grammar.FIRST(&header); if (first.size() <= 0) { continue; } bool empty = false; for (vector<Symbol *>::iterator f_itr = first.begin(); f_itr != first.end(); ++f_itr) { if (*f_itr == Symbol::EmptySymbolPtr()) { empty = true; } int f_key = (*f_itr)->identifier(); int col_index = col_map[f_key]; table[row_index][col_index] = index; } /// 2. 如果FIRST中包含有空串时,FOLLOW(A)中每个终结符号b,将产生式 A --> α 加入到 table[A][b] 中 /// 3. 如果结束符号$在FOLLOW(A)中,将产生式 A --> α 加入到 table[A][$] 中 if (!empty) { return; } vector<Symbol *>follows = grammar.FOLLOW(&header); for (vector<Symbol *>::iterator f_itr = follows.begin(); f_itr != follows.end(); ++f_itr) { int f_key = (*f_itr)->identifier(); int col_index = col_map[f_key]; table[row_index][col_index] = index; } } } public: ll_prediction_analysis_table(ContextFreeGrammar& grammar) { this->grammar = grammar; extract_symbol(); create_table(); } Production& objectForPair(pair<Symbol*, Symbol*> row_col); };
|
四、非递归的预测分析
我们可以显式地维护一个栈结构,来构造出一个非递归的预测分析器。如下图所示:
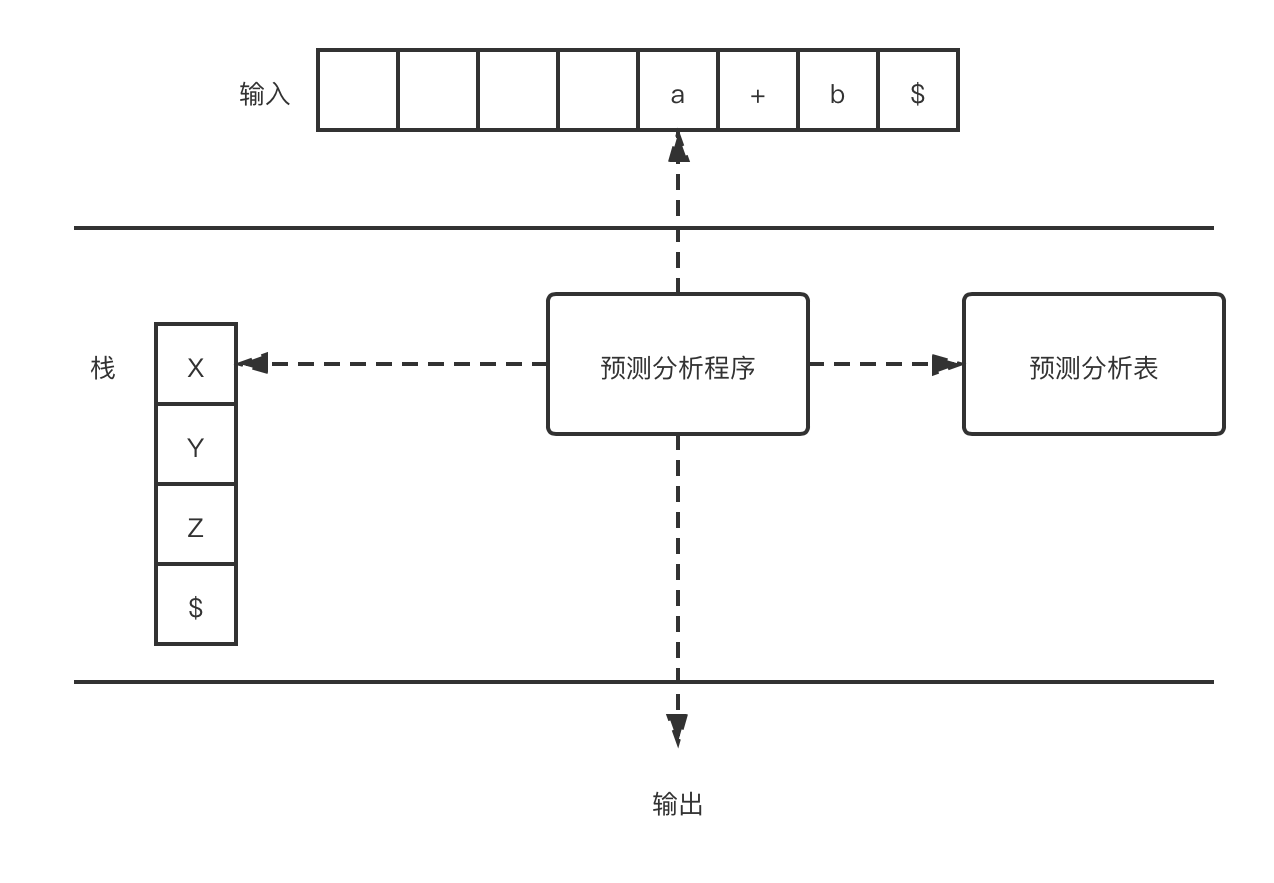
上图中的语法分析器有一个输入缓冲区,一个包含了文法符号序列的栈,一个上一节我们学习到的语法分析表,以及一个输出流。其中输入缓冲区中包含要进行语法分析的串。
其大致的执行过程如下:
1)、考虑栈顶符号X和当前输入符号a;
2)、如果X是一个非终结符号,该分析器查询预测分析表M中的条目M[X,a]来选择一个产生式;
3)、如果X不是一个非终结符号,那么检查终结符号X和当前的输入符号a是否匹配;
下面是表驱动的预测分析方法伪代码,其中输入为待匹配的字符串,和一个预测分析表;上图中栈第一个元素值为文法的开始符号,栈底存在一个哨兵,用于判断当前栈是否为空:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
| bool ll_syntax::syntax() { Symbol *ended = const_cast<Symbol *>(Symbol::EndedSymbolPtr()); char* ip = &input_string[0]; for (Symbol *sym = stack.back(); sym->identifier() != ended->identifier(); sym = stack.back()) { if (sym->identifier() == *ip) { stack.pop_back(); ip++; continue; } if (sym->isTerminal()) { return false; /// 语法错误 } Terminal ip_sym(*ip); int status = 0; Production prodction = table.objectForPair(make_pair(sym, &ip_sym), &status); if (status != 0) { return false; /// 语法错误 } /// 移除栈顶元素,然后将产生式体加入到栈中 stack.pop_back(); vector<Symbol *> bodies = prodction.bodies; for (vector<Symbol *>::const_reverse_iterator itr = bodies.rbegin; itr != bodies.rend(); ++itr) { stack.push_back(*itr); } } return true; }
|
这儿我用代码简单地实现了一下,到这儿我们基本上把LL语法分析初步学习完了。 本篇文章中最主要部分还是对产生式求解FIRST集合和FOLLOW集合,这个是务必要掌握的,切记切记!!!






