简单了解2-3树、2-3-4树和红黑树

q.data = p.data_l;
q->left_child = p->left_child;
q->right_child = p->left_mid_child;

typedef struct red_black_tree* red_black_ptr;
typedef struct red_black_tree {
        element data;
        /// 左右儿子
        red_black_ptr left_child;
        red_black_ptr right_child;
        /// 两个颜色域
        color left_color;
        color right_color;
}red_black;

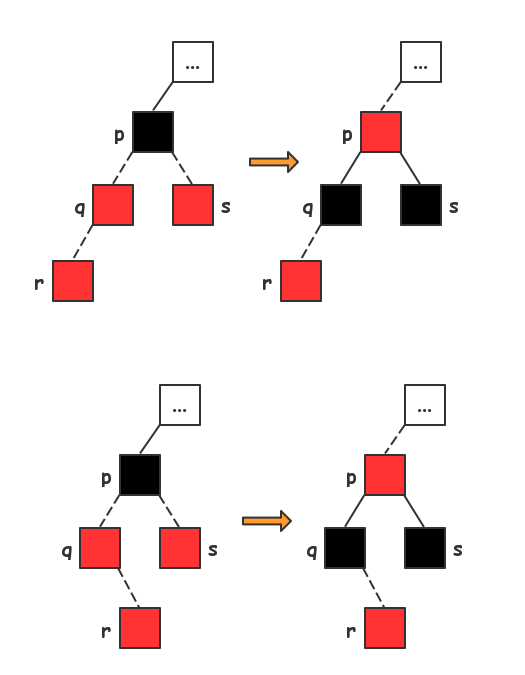
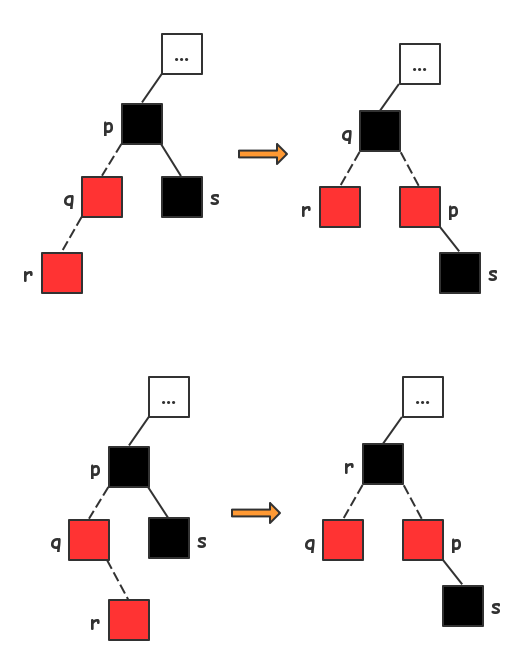
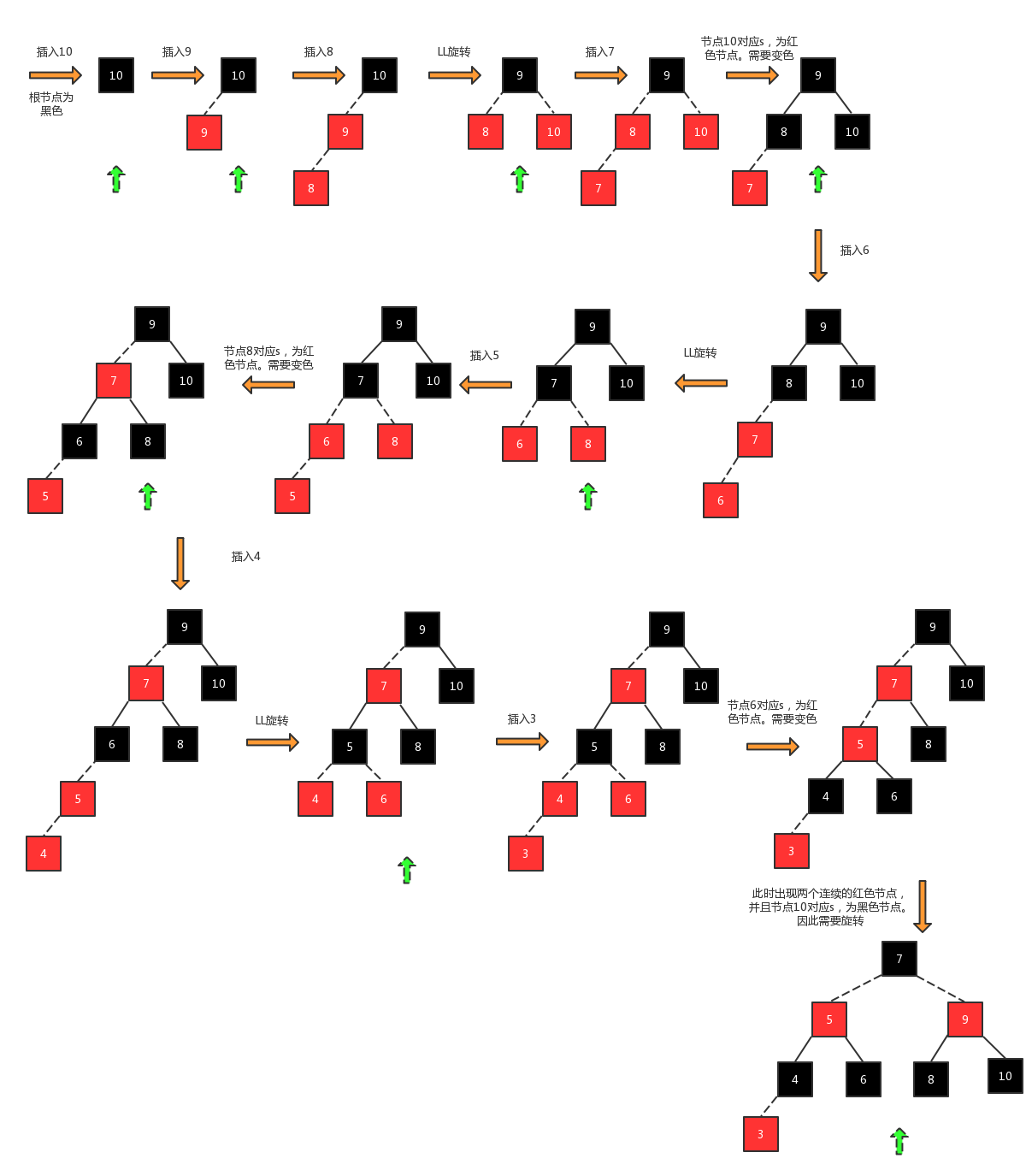
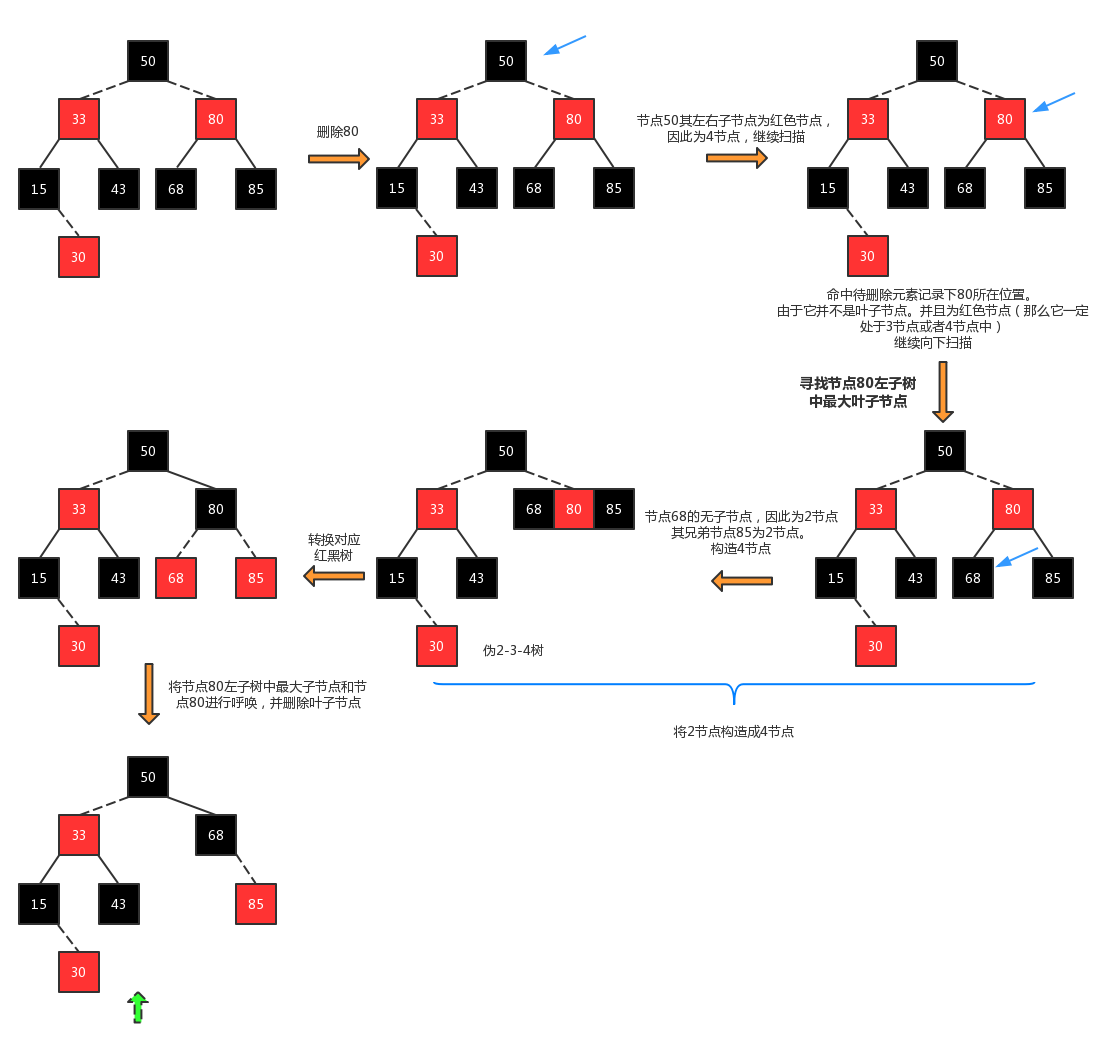
#include <iostream>
#include <stdio.h>
#include <list>
#include <stdlib.h>
#include <cstdlib>
#include <algorithm>
#include <ctime>
#include <set>
#include <vector>
using namespace std;
/// 这里假设对于element来说，如果该域值不存在，我们使得element的value部分设置为INT_MAX
class element {
private:
	int value;
public:
	element(int val) :value(val) {}
	element() { value = INT_MAX; }
	void setValue(int val) {value = val;}
	int getValue() const { return value; }
	static inline element invalid() {
		return element(INT_MAX);
	}
};
bool operator == (const element& lhs,const element& rhs) {
	return lhs.getValue() == rhs.getValue();
}
bool operator != (const element& lhs,const element& rhs) {
	return !(lhs.getValue() == rhs.getValue());
}
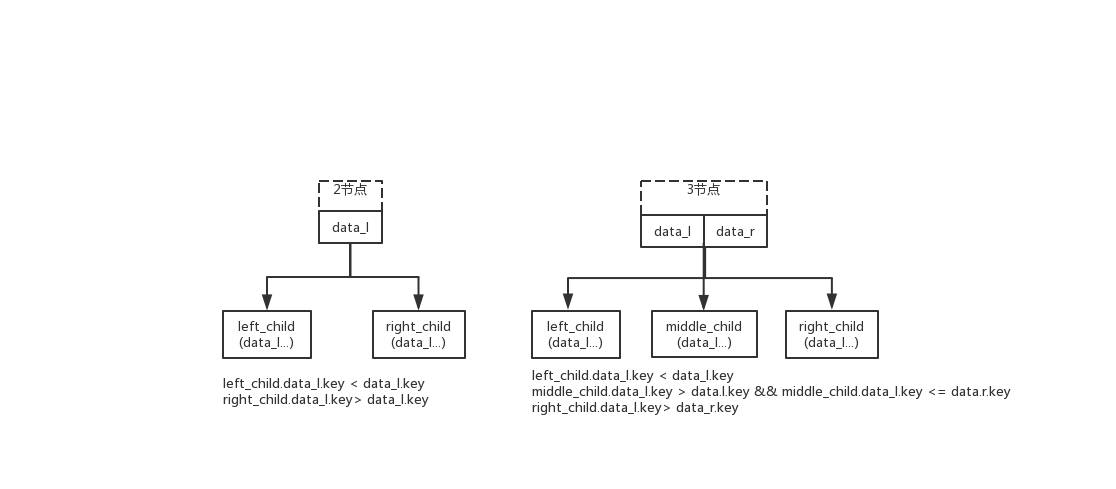
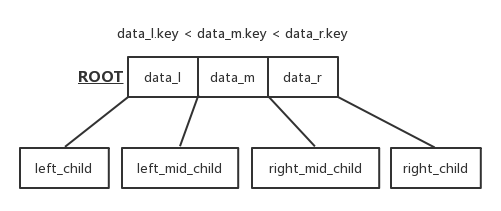
class two_three_tree_node {
public:
	element data_l;
	element data_r;
	two_three_tree_node* left_child;
	two_three_tree_node* middle_child;
	two_three_tree_node* right_child;
public:
	two_three_tree_node()
	{
		data_l = element::invalid();
		data_r = element::invalid();
		left_child = NULL;
		middle_child = NULL;
		right_child = NULL;
	}
	virtual ~two_three_tree_node()
	{
		data_l = element::invalid();
		data_r = element::invalid();
		if (left_child != nullptr)
		{
			delete left_child;
		}
		if (middle_child != nullptr)
		{
			delete middle_child;
		}
		if (right_child != nullptr)
		{
			delete right_child;
		}
	}
};
class node_strategy {
protected:
	const two_three_tree_node* node;
	element value;
public:
	node_strategy():node(NULL),value(element::invalid()) {
	}
	virtual void setValue(const element& ele) = 0;
	virtual void setNode(const two_three_tree_node* nd) = 0;
	virtual two_three_tree_node* next() = 0;
	virtual ~node_strategy()
	{
	}
};
class left_child_strategy:public node_strategy {
	two_three_tree_node* next() {
		element data_left = node->data_l;
		if (value.getValue() < data_left.getValue()) { return node->left_child; }
		return nullptr;
	}
	void setValue(const element& ele) {
		value = ele;
	}
	void setNode(const two_three_tree_node* nd) {
		node = nd;
	}
};
class middle_child_strategy :public node_strategy {
	two_three_tree_node* next() {
		element data_left = node->data_l;
		element data_right = node->data_r;
		if (value.getValue() > data_left.getValue() && value.getValue() < data_right.getValue()) { return node->middle_child; }
		return nullptr;
	}
	void setValue(const element& ele) {
		value = ele;
	}
	void setNode(const two_three_tree_node* nd) {
		node = nd;
	}
};
class right_child_strategy :public node_strategy {
	two_three_tree_node* next() {
		element data_right = node->data_r;
		if (value.getValue() > data_right.getValue()) {
			return node->right_child;
		}
		return nullptr;
	}
	void setValue(const element& ele) {
		value = ele;
	}
	void setNode(const two_three_tree_node* nd) {
		node = nd;
	}
};
///#######################################################################################################################
///#######################################################################################################################
/// #### 查找
///#######################################################################################################################
///#######################################################################################################################
class search_strategy {
	two_three_tree_node* root;
public:
	search_strategy(two_three_tree_node* rt) {
		root = rt;
	}
	two_three_tree_node* search(element& ele) {
		two_three_tree_node* node = root;
		node_strategy *left = new left_child_strategy();
		node_strategy *middle = new middle_child_strategy();
		node_strategy *right = new right_child_strategy();
		while (node)
		{
			if (node->data_l == ele)
			{
				return node;
			}
			if (node->data_r == ele)
			{
				return node;
			}
			left->setNode(node);
			left->setValue(ele);
			if (two_three_tree_node *temp = left->next())
			{
				node = temp;
				continue;
			}
			middle->setNode(node);
			middle->setValue(ele);
			if (two_three_tree_node * temp = middle->next())
			{
				node = temp;
				continue;
			}
			right->setNode(node);
			right->setValue(ele);
			if (two_three_tree_node * temp = right->next())
			{
				node = temp;
				continue;
			}
			node = nullptr;
		}
		delete left;
		delete middle;
		delete right;
		return nullptr;
	}
};
///#######################################################################################################################
///#######################################################################################################################
/// #### 插入
///#######################################################################################################################
///#######################################################################################################################
class insert_strategy {
private:
	/// 创建一个栈结构，将从叶节点到根节点路径上左右的节点保存下来
	struct find_stack {
		struct find_stack_node {
			two_three_tree_node* tree_node;
			find_stack_node* next;
		};
		void push(const two_three_tree_node* tree_node) {
			if (!tree_node)
			{
				return;
			}
			find_stack_node* node = new find_stack_node();
			node->tree_node = const_cast<two_three_tree_node*>(tree_node);
			node->next = top;
			top = node;
		}
		two_three_tree_node* pop() {
			find_stack_node* node = top;
			top = top->next;
			two_three_tree_node* tree_node = node->tree_node;
			node->next = nullptr;
			node->tree_node = nullptr;
			delete node;
			return tree_node;
		}
		find_stack_node* stack_top() {
			return top;
		}
		~find_stack()
		{
			while (top)
			{
				pop();
			}
		}
	private:
		find_stack_node* top;
	};
///#######################################################################################################################
///#######################################################################################################################
///#####寻找节点
///#######################################################################################################################
///#######################################################################################################################
	class find_element {
	private:
		two_three_tree_node* root;
		element value;
		find_stack* stack;
	public:
		find_element(const two_three_tree_node* rt, element val) {
			root = const_cast<two_three_tree_node*>(rt);
			value = val;
			stack = new find_stack();
		}
		void set_value(element val) {
			value = val;
		}
		/// 修改版查找：根据根节点和指定元素：如果查找到指定元素，则认为查找成功，返回null；否则返回查找过程中遇到的叶子节点；
		two_three_tree_node* node() {
			two_three_tree_node* node = root;
			node_strategy* left = new left_child_strategy();
			node_strategy* middle = new middle_child_strategy();
			node_strategy* right = new right_child_strategy();
			two_three_tree_node* result = nullptr;
			while (node)
			{
				stack->push(node);
				if (node->data_l == value)
				{
					goto release;
				}
				if (node->data_r == value)
				{
					goto release;
				}
				left->setNode(node);
				left->setValue(value);
				if (two_three_tree_node * temp = left->next())
				{
					node = temp;
					continue;
				}
				middle->setNode(node);
				middle->setValue(value);
				if (two_three_tree_node * temp = middle->next())
				{
					node = temp;
					continue;
				}
				right->setNode(node);
				right->setValue(value);
				if (two_three_tree_node * temp = right->next())
				{
					node = temp;
					continue;
				}
				node = nullptr;
			}
			if (stack->stack_top())
			{
				result = stack->stack_top()->tree_node;
			}
			release:
			delete left;
			delete middle;
			delete right;
			return result;
		}
		find_stack* get_stack() {
			return stack;
		}
		~find_element()
		{
			root = nullptr;
			delete stack;
			stack = nullptr;
		}
	};
	//// 拼接
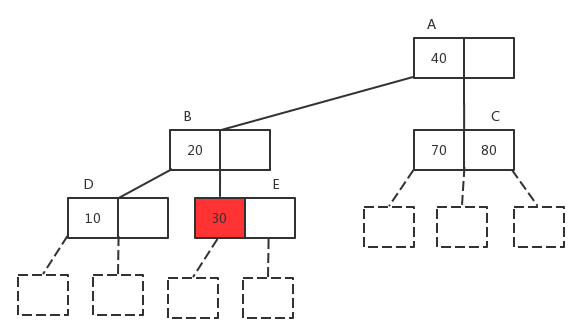
	class split_element {
	private:
		find_stack* stack;
		element ele;
	public:
		split_element(const find_stack* steck,const element& val) {
			stack = const_cast<find_stack *>(steck);
			ele = val;
		}
		
		two_three_tree_node* split(bool (*two_node_insert_handle)(two_three_tree_node* node,const two_three_tree_node* insert_node)){
			find_stack::find_stack_node* top = stack->stack_top();
			two_three_tree_node* be_insert_node = new two_three_tree_node();
			be_insert_node->data_l = ele;
			int breakpoint = ele.getValue();
			while(be_insert_node->data_l != element::invalid() && top){
				two_three_tree_node* current = top->tree_node;
				if (two_node_insert_handle(current, be_insert_node)) {
					return nullptr;
				}
				/// current 存放三个元素里面最小的一个
				/// max 存放三个元素里面最大的一个
				two_three_tree_node* max_item = new two_three_tree_node();
				if (be_insert_node->data_l.getValue() < current->data_l.getValue())
				{
					max_item->data_l = current->data_r;
					max_item->data_r = element::invalid();
					max_item->left_child = current->middle_child;
					max_item->middle_child = current->right_child;
					element temp = current->data_l;
					current->data_l = be_insert_node->data_l;
					current->data_r = element::invalid();
					current->left_child = be_insert_node->left_child;
					current->middle_child = be_insert_node->middle_child;
					current->right_child = nullptr;
					
					be_insert_node->data_l = temp;
					be_insert_node->data_r = element::invalid();
					be_insert_node->left_child = current;
					be_insert_node->middle_child = max_item;
					top = top->next;
					continue;
				}
				if (be_insert_node->data_l.getValue() > current->data_r.getValue()) {
					max_item->data_l = be_insert_node->data_l;
					max_item->data_r = element::invalid();
					max_item->left_child = be_insert_node->left_child;
					max_item->middle_child = be_insert_node->middle_child;
					current->right_child = nullptr;
					element temp = current->data_r;
					current->data_r = element::invalid();
					be_insert_node->data_l = temp;
					be_insert_node->left_child = current;
					be_insert_node->middle_child = max_item;
					be_insert_node->data_r = element::invalid();
					top = top->next;
					continue;
				}
				if (be_insert_node->data_l.getValue() < current->data_r.getValue() && be_insert_node->data_l.getValue() > current->data_l.getValue()) {
					max_item->data_l = current->data_r;
					max_item->left_child = be_insert_node->middle_child;
					max_item->middle_child = current->right_child;
					max_item->data_r = element::invalid();
					current->middle_child = be_insert_node->left_child;
					current->data_r = element::invalid();
					current->right_child = nullptr;
					be_insert_node->left_child = current;
					be_insert_node->middle_child = max_item;
					be_insert_node->right_child = nullptr;
					be_insert_node->data_r = element::invalid();
					top = top->next;
					continue;
				}
			}
			return be_insert_node;
		}
	};
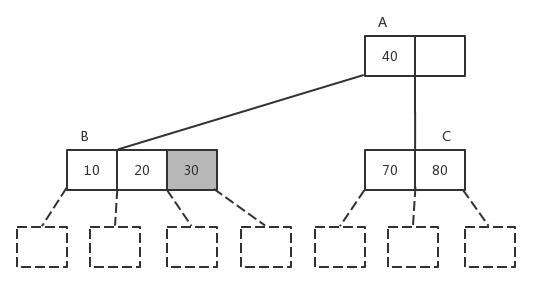
	static bool two_node_insert(two_three_tree_node* node, const two_three_tree_node* insert_node) {
		if (node->data_r != element::invalid())
		{
			return false;
		}
		
		if (node->data_l.getValue() < const_cast<two_three_tree_node*>(insert_node)->data_l.getValue())
		{
			node->data_r = insert_node->data_l;
			node->middle_child = insert_node->left_child;
			node->right_child = insert_node->middle_child;
		}
		else
		{
			element temp = node->data_l;
			node->data_l = insert_node->data_l;
			node->data_r = temp;
			node->right_child = node->middle_child;
			node->left_child = insert_node->left_child;
			node->middle_child = insert_node->middle_child;
		}
		return true;
	}
public:
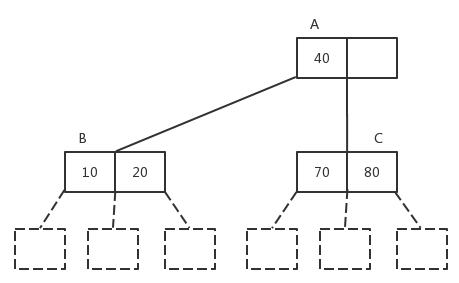
	two_three_tree_node* insert(two_three_tree_node* root ,const element &ele) {
		find_element* fele = new find_element(root,ele);
		two_three_tree_node* leaf = fele->node();
		if (nullptr == leaf)
		{/// 待插入元素已存在于树中
			delete fele;
			return root;
		}
		split_element* se = new split_element(fele->get_stack(), ele);
		two_three_tree_node* root_node = se->split(two_node_insert);
		if (root_node == nullptr) {/// 2节点
			delete fele;
			return root;
		}
		/// 3节点
		delete fele;
		return root_node;
	}
};
///#######################################################################################################################
///#######################################################################################################################
/// #### 删除
///#######################################################################################################################
///#######################################################################################################################
class delete_strategy {
	two_three_tree_node* root;
	element ele;
private:
	/// 获取兄弟节点;
	two_three_tree_node* get_bro_node(two_three_tree_node * const node, two_three_tree_node * const parent) {
		if (node == parent->left_child)
		{
			return parent->middle_child;
		}
		if (node == parent->middle_child)
		{
			if (is_three_node(parent->right_child))
			{
				return parent->right_child;
			}
			return parent->left_child;
		}
		if (node == parent->right_child) 
		{
			return parent->middle_child;
		}
		return nullptr;
	}
protected:
	static inline bool is_three_node(two_three_tree_node* node) {
		if (nullptr == node)
		{
			return false;
		}
		if (node->data_l != element::invalid() && node->data_r != element::invalid())
		{
			return true;
		}
		return false;
	}
	static bool remove_element(two_three_tree_node* node, element ele) {
		if (node->data_r == ele)
		{
			node->data_r = element::invalid();
			return true;
		}
		if (node->data_l == ele) {
			node->data_l = node->data_r;
			node->data_r = element::invalid();
			return true;
		}
		return false;
	}
	class delete_ttt_node {
	public:
		two_three_tree_node* node;
		element* isptr;
		delete_ttt_node(const two_three_tree_node* rt, const element* is) {
			node = const_cast<two_three_tree_node*>(rt);
			isptr = const_cast<element*>(is);
		}
	};
	/// 叶节点转移
	class leaf_swap {
		delete_ttt_node* ttt_node;
		element ele;
		/// 返回值为目标节点
		/// leaf为叶节点
	private:
		two_three_tree_node* leaf_node;
		two_three_tree_node* leaf_parent_node;
	public:
		leaf_swap(const two_three_tree_node* rt, element& el) {
			ttt_node = new delete_ttt_node(rt, nullptr);
			ele = el;
			leaf_node = nullptr;
			leaf_parent_node = nullptr;
		}
		leaf_swap() {
			ttt_node = new delete_ttt_node(nullptr, nullptr);
			ele = element::invalid();
			leaf_node = nullptr;
			leaf_parent_node = nullptr;
		}
		~leaf_swap()
		{
			delete ttt_node;
		}
		two_three_tree_node* get_leaf_node() {
			return leaf_node;
		}
		two_three_tree_node* get_leaf_parent_node() {
			return leaf_parent_node;
		}
		delete_ttt_node* get_swap_info(two_three_tree_node** leaf) {
			two_three_tree_node* node = ttt_node->node;
			delete_ttt_node* des_node = new delete_ttt_node(ttt_node->node, nullptr);
			node_strategy* left = new left_child_strategy();
			node_strategy* middle = new middle_child_strategy();
			node_strategy* right = new right_child_strategy();
			/// 命中待删除元素
			while (node)
			{
				if (node->data_l == ele)
				{
					des_node->node = node;
					des_node->isptr = &(node->data_l);
					break;
				}
				if (node->data_r == ele)
				{
					des_node->node = node;
					des_node->isptr = &(node->data_r);
					break;
				}
				left->setNode(node);
				left->setValue(ele);
				if (two_three_tree_node * temp = left->next())
				{
					leaf_parent_node = node;
					node = temp;
					continue;
				}
				middle->setNode(node);
				middle->setValue(ele);
				if (two_three_tree_node * temp = middle->next())
				{
					leaf_parent_node = node;
					node = temp;
					continue;
				}
				right->setNode(node);
				right->setValue(ele);
				if (two_three_tree_node * temp = right->next())
				{
					leaf_parent_node = node;
					node = temp;
					continue;
				}
				node = nullptr;
			}
			delete left;
			delete middle;
			delete right;
			/// 寻找叶子节点
			/// 左子树的最大子节点；或者右子树的最小子节点；
			/// 这里我选择左子树的最大子节点；
			if (des_node == nullptr)
			{
				leaf_parent_node = nullptr;
				return des_node;
			}
			*leaf = des_node->node;
			
			for (node = (des_node->isptr->getValue() == des_node->node->data_r.getValue()) ? des_node->node->middle_child : des_node->node->left_child;
				node; 
				node = node->middle_child)
			{
				/// 非叶节点
				leaf_parent_node = *leaf;
				*leaf = node;
			}
			return des_node;
		}
		bool swap() {/// 仅仅交换两个指针的数据域的值，指针域不做改变
			two_three_tree_node* leaf = nullptr;
			delete_ttt_node* des_node = get_swap_info(&leaf);
			leaf_node = leaf;
			if (nullptr == des_node || nullptr == leaf)
			{
				return false;
			}
			if (des_node->node == leaf)
			{/// 叶节点，不做交换
				return true;
			}
			if (leaf->data_r != element::invalid())
			{
				element r_temp = leaf->data_r;
				leaf->data_r = *(des_node->isptr);
				*(des_node->isptr) = r_temp;
			}
			else 
			{
				element l_temp = leaf->data_l;
				leaf->data_l = *(des_node->isptr);
				*(des_node->isptr) = l_temp;
			}
			delete des_node;
			return true;
		}
	};
	class two_node_delete_interface {
	protected:
		two_three_tree_node* leaf;
		two_three_tree_node* bro;
		two_three_tree_node* parent;
		two_node_delete_interface(two_three_tree_node* lf, two_three_tree_node* bo, two_three_tree_node* pt) :leaf(lf), bro(bo), parent(pt) {}
		virtual ~two_node_delete_interface(){}
	};
	/// 旋转
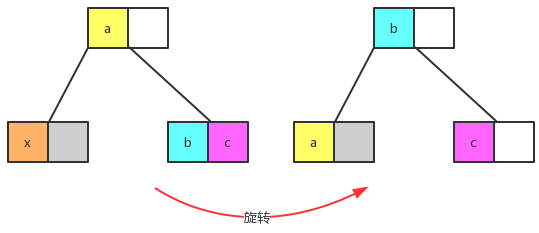
	class rotate : public two_node_delete_interface {/// 兄弟节点为3节点时，旋转
	private:
		bool left_leaf_rotate() {
			leaf->data_l = parent->data_l;
			leaf->data_r = element::invalid();
			parent->data_l = bro->data_l;
			bro->data_l = bro->data_r;
			bro->data_r = element::invalid();
			leaf->middle_child = bro->left_child;
			bro->left_child = bro->middle_child;
			bro->middle_child = bro->right_child;
			return true;
		}
		bool right_leaf_rorate() {
			leaf->data_l = parent->data_l;
			parent->data_l = bro->data_r;
			leaf->left_child = bro->right_child;
			return true;
		}
		bool middle_leaf_rorate() {
			if (bro == parent->right_child) {
				leaf->data_l = parent->data_r;
				leaf->data_r = element::invalid();
				parent->data_r = bro->data_l;
				bro->data_l = bro->data_r;
				bro->data_r = element::invalid();
				leaf->middle_child = bro->left_child;
				bro->left_child = bro->middle_child;
				bro->middle_child = bro->right_child;
				return true;
			}
			leaf->data_l = parent->data_l;
			parent->data_l = bro->data_r;
			leaf->left_child = bro->right_child;
			return true;
		}
	public:
		rotate(two_three_tree_node* lf, two_three_tree_node* bo, two_three_tree_node* pt):two_node_delete_interface(lf, bo, pt) {}
		bool execute() {
			if (nullptr == leaf || nullptr == parent || nullptr == bro)
			{
				return false;
			}
			if (leaf == parent->left_child) 
			{
				return left_leaf_rotate();
			}
			else if (leaf == parent->middle_child)
			{
				return middle_leaf_rorate();
			}
			else 
			{
				return right_leaf_rorate();
			}
		}
	};
	/// 合并
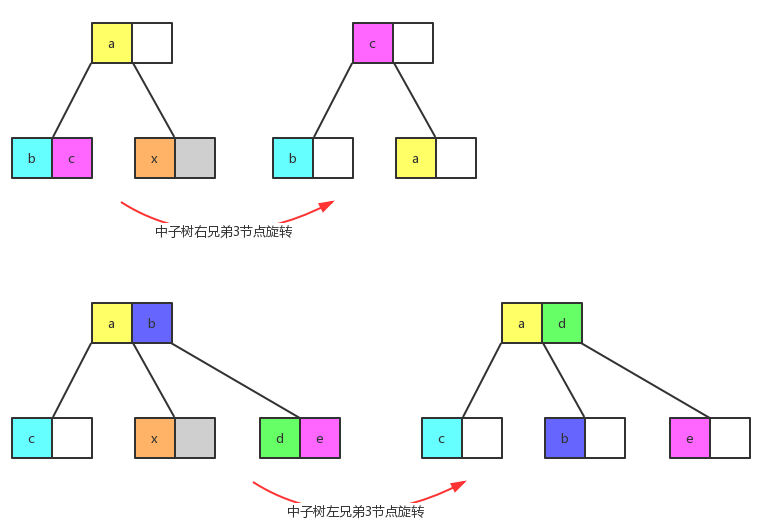
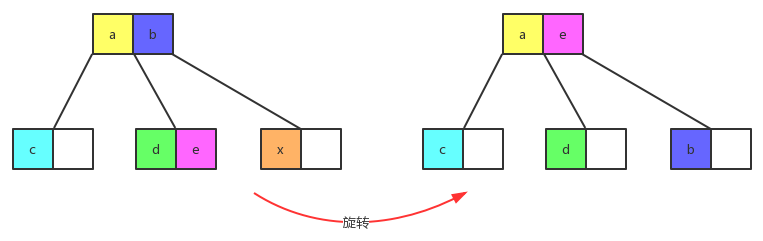
	class combine : public two_node_delete_interface {
	protected:
		bool left_leaf_combine() {
			if (nullptr == leaf || nullptr == parent || nullptr == bro)
			{
				return false;
			}
			bool parent_is_three_node = is_three_node(parent);
			if (false == parent_is_three_node)
			{
				parent->data_r = bro->data_l;
				parent->left_child = leaf->left_child;
				parent->middle_child = bro->left_child;
				parent->right_child = bro->right_child;
				delete bro;
				delete leaf;
				bro = nullptr;
				leaf = nullptr;
				return true;
			}
			bro->data_r = bro->data_l;
			bro->data_l = parent->data_l;
			parent->data_l = parent->data_r;
			parent->data_r = element::invalid();
			parent->left_child = parent->middle_child;
			parent->middle_child = parent->right_child;
			parent->right_child = nullptr;
			bro->right_child = bro->middle_child;
			bro->middle_child = bro->left_child;
			bro->left_child = leaf->left_child;
			delete leaf;
			leaf = nullptr;
			return true;
		}
		bool middle_leaf_combine() {
			if (nullptr == leaf || nullptr == parent || nullptr == bro)
			{
				return false;
			}
			bool parent_is_three_node = is_three_node(parent);
			if (false == parent_is_three_node)
			{
				parent->data_r = parent->data_l;
				parent->data_l = bro->data_l;
				parent->left_child = nullptr;
				parent->middle_child = nullptr;
				delete leaf;
				delete bro;
				leaf = nullptr;
				bro = nullptr;
				return true;
			}
			bro->data_r = parent->data_l;
			parent->data_l = parent->data_r;
			parent->data_r = element::invalid();
			parent->middle_child = parent->right_child;
			parent->right_child = nullptr;
			bro->middle_child = leaf->left_child;
			bro->right_child = leaf->middle_child;
			delete leaf;
			leaf = nullptr;
			return true;
		}
		bool right_leaf_combine() {
			if (nullptr == leaf || nullptr == parent || nullptr == bro)
			{
				return false;
			}
			bro->data_r = parent->data_r;
			parent->data_r = element::invalid();
			parent->right_child = nullptr;
			bro->middle_child = leaf->left_child;
			bro->right_child = leaf->middle_child;
			delete leaf;
			leaf = nullptr;
			return true;
		}
	public:
		combine(two_three_tree_node* lf, two_three_tree_node* bo, two_three_tree_node* pt) :two_node_delete_interface(lf, bo, pt) {}
		bool execute() {
			if (nullptr == leaf || nullptr == parent || nullptr == bro)
			{
				return false;
			}
			if (leaf == parent->left_child)
			{
				return left_leaf_combine();
			}
			else if(leaf == parent->middle_child)
			{
				return middle_leaf_combine();
			}
			else
			{
				return right_leaf_combine();
			}
		}
	};
	class two_node_delete : public two_node_delete_interface {
	public:
		two_node_delete(two_three_tree_node* lf, two_three_tree_node* bo, two_three_tree_node* pt):two_node_delete_interface(lf, bo, pt) {}
		bool execute() {
			if (nullptr == leaf || nullptr == parent || nullptr == bro)
			{
				return false;
			}
			/// 查看兄弟节点为2节点，还是3节点；
			bool three_node = is_three_node(bro);
			if (true == three_node) /// 兄弟节点为3节点，旋转
			{
				rotate* rtt = new rotate(leaf, bro, parent);
				return rtt->execute();
			}
			else  /// 兄弟节点为2节点，合并
			{
				combine* cbn = new combine(leaf, bro, parent);
				return cbn->execute();
			}
			return false;
		}
	};
public:
	delete_strategy(const two_three_tree_node*rt, element& el) {
		root = const_cast<two_three_tree_node*>(rt);
		ele = el;
	}
	bool execute() {
		leaf_swap* ls = new leaf_swap(root, ele);
		bool result = ls->swap();
		if (false == result)
		{
			return false;
		}
		two_three_tree_node* leaf = ls->get_leaf_node();
		if (nullptr == leaf)
		{
			return false;
		}
		two_three_tree_node* leaf_parent = ls->get_leaf_parent_node();
		/// 3节点
		if (is_three_node(leaf))
		{
			remove_element(leaf, ele);
			return true;
		}
		/// 2节点
		two_three_tree_node* bro = get_bro_node(leaf, leaf_parent);
		if (nullptr == bro)
		{
			return false;
		}
		two_node_delete* tnd = new two_node_delete(leaf, bro, leaf_parent);
		tnd->execute();
		return result;
	}
};
int main()
{
	vector<int> randoms;
	/// 插入
	//cout << "input root node value: " << endl;
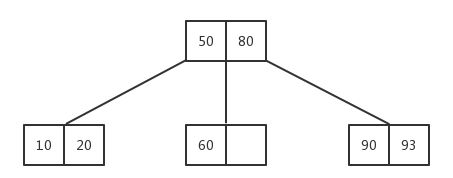
	int rootvalue = 50;
	//cin >> rootvalue;
	two_three_tree_node* root = new two_three_tree_node();
	root->data_l = element(rootvalue);
	/* 自行定制输入数字
	int inputvalue = 0;
	while (cout << "input node (-1 exit): ", cin >> inputvalue,inputvalue != -1)
	{
		randoms.push_back(inputvalue);
	}
	*/
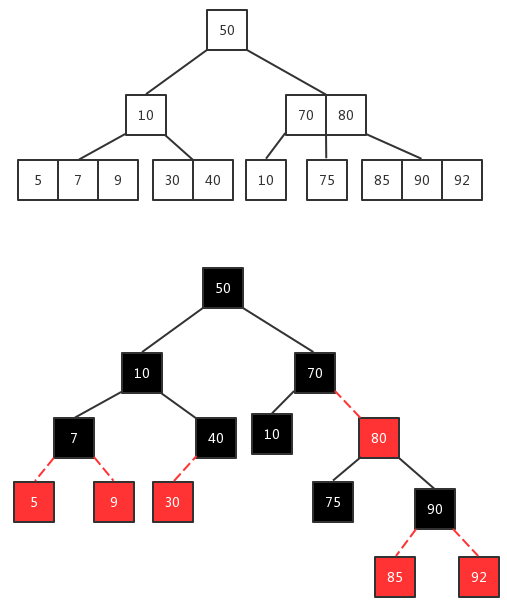
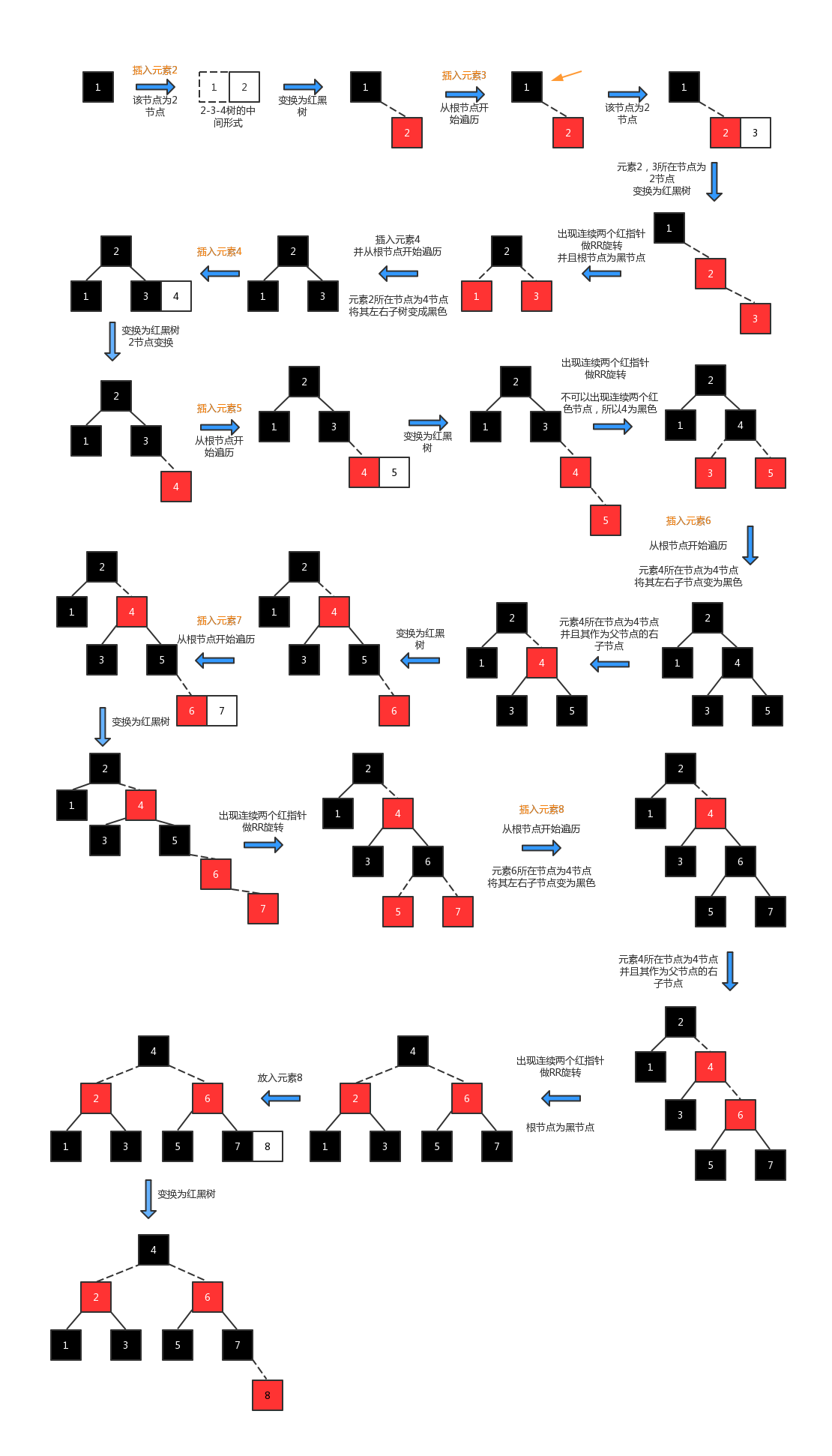
	randoms = { 33 ,85 ,68 ,80 ,62 ,15 ,97 ,10 };
	insert_strategy* ins = new insert_strategy();
	for (vector<int>::iterator itr = randoms.begin(); itr != randoms.end(); itr++)
	{
		root = ins->insert(root, element(*itr));
	}
	/// 查找
	search_strategy* search = new search_strategy(root);
	element search_item(12);
	bool search_result = search->search(search_item);
	/// 删除
	int val;
	while (cout<<"input delete item: "<<endl,cin>>val,val!=-1) {
		element be_deleted(val);
		delete_strategy* delete_s = new delete_strategy(root, be_deleted);
		delete_s->execute();
	}
	return 0;
}