词法分析——手动词法单元的识别（状态转换图、KMP算法）

在这儿我们先用手工的方式将正则表达式表示的模式转换为状态转换图。在下一节我们会用自动化的方法构造对应的转换图。

1）、结点：状态转换图有一组被称为“状态”的结点，它表示在扫描过程（即词法分析器扫描指定输入串，寻找指定模式词素）中可能出现的状态。也就是lexemeBegin指针和forward指针之间的所有的字符。
2）、边：从图的一个状态指向另一个状态，每条边的标号包含了一个或多个符号。如果找到这样的一条边，就将forward指针前移，并进入该边指向的下一个状态。
3）、开始状态：也就是上图中的start。
4）、接收状态或者最终状态：该状态表明已经找到了一个词素。也就是上图中两个圆圈。

接收状态通常是 向语法分析器返回一个词法单元和相关的属性值 。

5）、回退🌟号：上图中接受状态右上角的*号，表示我们识别到的词素并不包含使我们到达接受状态的符号（也就是上图中的no let/dig边）。此时我们需要回退forward指针到倒数第二个状态。这其中可能会回退多步，所以这里用*号来表示需要回退；

relop状态转换图

我们根据上一节的relop词法单元，已经对应的属性来构造一个relop的状态转换图

词素	词法单元名字	属性值
<	relop	LT
>	relop	GT
…	…	…
!=	relop	NE

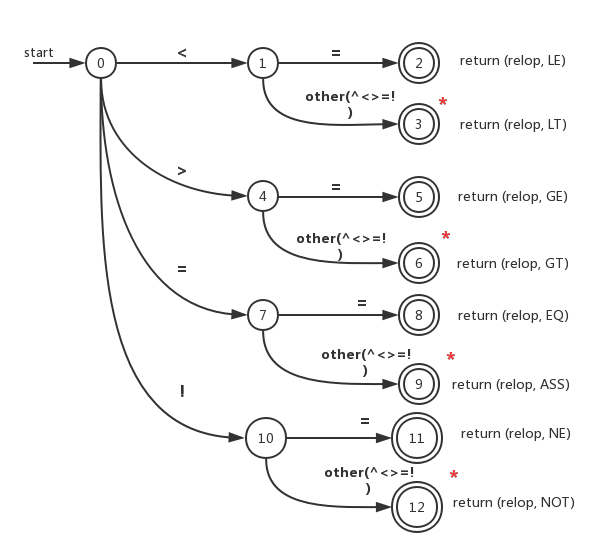
其实对于这个状态转换图来说，我只画了其中的比较运算符和逻辑运算符。对于位运算符（<<左移, >>右移）并没画出来。这里主要是想表达各个接收状态，和forward指针回退的操作。

id（标识符）和关键字的状态转换图

词法单元	模式
letter	[A-Za-z]
id	letter(letter , digit)*

注：上表中的正则表达式将逗号“,”更改为”|”。
对于关键字来说，它们看起来和标识符是很像的。但它们并不是标识符。

对于关键字if/else/for等等关键字，标识符forearm同样也是满足上诉转换图的。

为了解决上诉问题，编译原理中的处理方案有两个：

（1）👏👏👏、初始化时就将各个保留字填入符号表中；
符号表的某个字段会指明这些串并不是普通的标识符，并指出其对应的词法单元。
当我们找到一个标识符时，如果该标识符尚未出现在符号表中，就会调用上图中出现的installID将此标识符放入符号表中，并返回一个指针（该指针指向词素对应的符号表条目）。

任何在词法分析时不在符号表中的标识符都不可能是一个保留字，因此它的词法单元是id

（2）、为每一个关键字建立单独的状态转换图；

对于这个状态图来说，我们必须要区分以else为前缀的标识符（比如elseid），因此我们在倒数第二个状态后的边，必须要限制为非字符和数字。

使用第二个方案时：必须要设定词法单元的优先级，使得当一个词素同时匹配id和保留字模式时，优先识别保留字词法单元。

我们从第一点可以确定标识符加入符号表的时机是：

识别到对应词法单元时，如果该标识符尚未加入符号表。此时词法分析器会将该 标识符 (也可以理解为词素) 放入符号表中。

词法单元number状态转换图

词法单元	模式
digit	[0-9]
digits	digit+
number	digits(.digits)?(E[+-]?digits)?

下图是一个识别整数和浮点数的状态转换图：

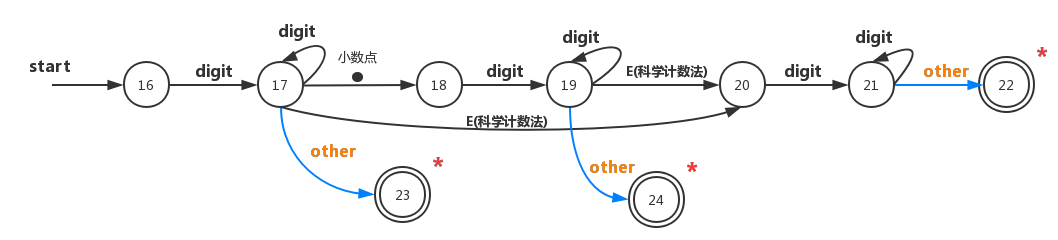
从上图中我们可以看到，接收状态22既匹配到了科学计数法表示的浮点数（包含小数部分，也包含指数部分），也匹配到了科学计数法表示的整数。
接收状态23是匹配到的整数词素；接收状态24为不带科学计数法的的整数。

当我们在接收状态时，返回词法单元 number 以及一个指向 常量表 条目的指针，上面找到的词素就放在这个常量表条目中。

ws（空白符）状态转换图

词法单元	模式
ws(空白符)	(blank \	tab \	newline)+

我们用转换delim替换上表中的blank、tab、newline：

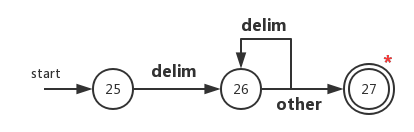
空白符后面需要跟一个非空白符才能确定当前已经完成了对连续空白符的扫描。

当我们识别到空白符之后，但我们 并不向语法分析器返回任何词法单元。相反，我们必须在这个空白符之后再次启动词法分析过程 。

基于状态转换图的的词法分析器体系结构

1、使用一个state变量来保存一个状态转换图的当前状态编号（就是前面我们从0到27的编号）。
2、用switch语句根据state的值将我们转到对应状态相应的代码段，该代码段为对应状态所需要执行的动作；

二、KMP算法

现在我们看一下KMP算法，它可以用于在文本串中识别一组关键字。在看KMP字符串匹配算法之前，我们先看一下朴素字符串匹配算法。

朴素字符串匹配算法

朴素字符串匹配算法是同一个循环找到所有有效偏移，寻找满足条件的情况。

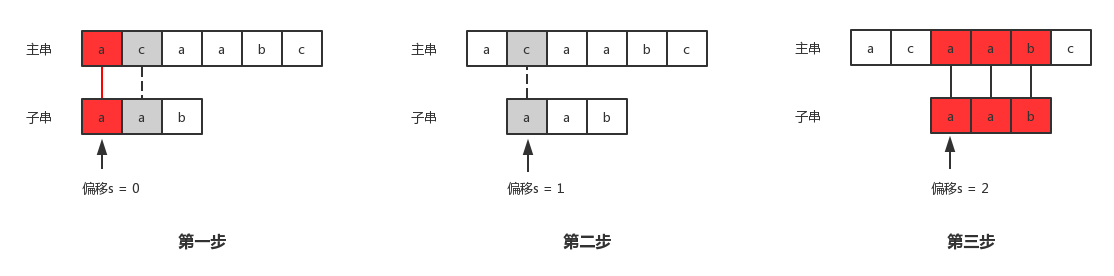
朴素字符串匹配算法可以形象地看成是待匹配串（子串）沿着原文本（主串）滑动，同时对每个偏移都要检测子串上的字符是否与主串中对应字符相等。其中红色字符表示对应位置匹配成功，灰色字符表示匹配失败。
大致的代码是这样：

using namespace std;
int naive_string_matcher(string text, string pattern)
{
     string::size_type n = text.size();
     string::size_type m = pattern.size();
     string::size_type total = n-m;
     string::size_type s = -1;
     for (string::size_type i = 0; i < total; i++)
     {
         s = i;
         string::size_type matched = 0;
         for(string::size_type idx = 0; idx < m; idx++)
         {
             if(pattern[idx] == text[s+idx]) matched++;
         }
         if (matched == m) return s;
     }
     return s;
 }

在最坏情况下，朴素字符串匹配算法的平均时间复杂度为O(n²) 。

失效函数

KMP算法在最坏情况下也会比朴素字符串匹配算法好很多。为了快速处理文本串并在这些串中搜索一个关键字，定义了 失效函数 f(s) ，其中s为对应状态图上的各个状态。也可以叫做辅助函数。
在这之前我们先看看串的一部分术语：

前缀：从串s尾部删除0个或多个符号后得到的串；
后缀：从串s开始处删除0个或多个符号后得到的串；
子串：删除某个前缀或者后缀之后得到的串；
真前缀、真后缀、真子串：指的是既不包含空串，也不包含本身的前缀、后缀、子串；

针对关键字b₁b₂b₃…b_n，其目标是使得b₁b₂…b_f(s)不仅是b₁…b_s的真前缀，又是b₁…b_s后缀的子串。并且b₁b₂…b_f(s)是所求得的最长串。下面我们以串ababaca来进行讲解：

a、构造关键字状态转换图

我们根据前面的知识，节点表示状态，有向边指的是转换

现在有了状态转换图，我们需要构造每一个状态节点s，所对应的失效函数值。

b、求解每一个状态s的函数值

1）、由于前面提到过真前缀的前提，因此我们从s=1开始计算。首先我们将f(1)设置为0，既状态1对应的失效函数值为0。并且这里我们新增一个辅助游标t用于对照状态s：

s	1	2	3	4	5	6	7
f(s)	0	-	-	-	-	-	-

2）、此时我们比较一下状态t的转换（a）和状态s的转换（b），发现字符a并不等于字符b。此时我们将f(s+1)，即f(2)的值设置为0：

s	1	2	3	4	5	6	7
f(s)	0	0	-	-	-	-	-

并且将s移动到状态2：

3）、继续比较状态t的转换（a）和状态s的转换（a）此时他们相等。因此 先将t的自增1，然后将f(s+1)，即f(2)的值设置为t的值（此时为1）：

s	1	2	3	4	5	6	7
f(s)	0	0	1	-	-	-	-

同样的，此时将s移动到状态3：

4）、依次比较后续的s=3，和s=4的情况。它们的情形和第三步类似：

s	1	2	3	4	5	6	7
f(s)	0	0	1	2	3	-	-

此时t=3，s=5。对应的状态转换图为：

5）、现在我们比较一下状态t的转换（b）和状态s的转换（c），它们并不相等。由于 此时t不为0，说明在此之前肯定是存在某一串既为真前缀，又为后缀子串 。因此我们获取t当前位置对应失效函数函数的值。
此时t=3，查上表可知f(3)=1。所以现在我们将t移动到状态1：

6）、同样的比较状态t的转换（b）和状态s的转换（c），依然不相等。
由于t不等于0，此时t=1，查第4步的表可知f(1)=0。所以我们现在将t移动到状态0：

7）、对于后续状态的失效函数值确定，可以仿照第2、3和5步进行求解。最终完整失效函数为：

s	1	2	3	4	5	6	7
f(s)	0	0	1	2	3	0	1

下面是对应的代码：

#include <iostream>
#include <string>
#include <vector>
using namespace std;
void trie_func(string pattern, vector<int> &f) {
	const string::size_type length = pattern.size()+1;
	int t = 0;
	f[0]=t;// f[0] store t
	f[1]=0;
	for(int s = 1; s< length-1; s++)	
	{
		while(t>0 && pattern[t] != pattern[s]){ t=f[t]; f[0]=t;  }	
		if(pattern[s]==pattern[t]){ t=t+1; f[s+1]=t; f[0]=t; }
		else {f[s+1]=0;}
	}
}
int main(int argc, const char * argv[]){
	string pattern("ababaca");
	vector <int> trie(pattern.size()+1);
	trie_func(pattern,trie);
	for (vector<int>::iterator itr = trie.begin(); itr != trie.end(); itr++) {
		cout<<*itr<<endl;
	}
	return 0;
}

子串与主串的比较

现在我们以主串bcbababaababacacd 和子串 ababaca 作为例子，来看主串是否包含子串。

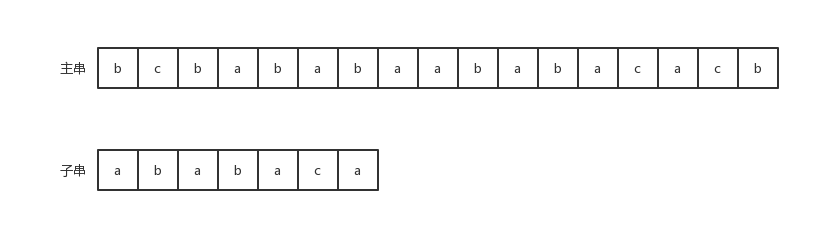
我们从前面知道子串失效函数为：

state	1	2	3	4	5	6	7
f(s)	0	0	1	2	3	0	1

这里我将上一节的字符s替换为state，是因为这一节我会用字符s用作当前子串相对于主串的偏移量。而真正原因是我太懒了，发现图中和失效函数都用了同一个字符s。为了避免混淆，但又不想重新画图🤣。

1）、主串的第一个字符和子串的第一个字符不相等。此时我们将子串向右滑动一位，此时偏移值s = 1 ：

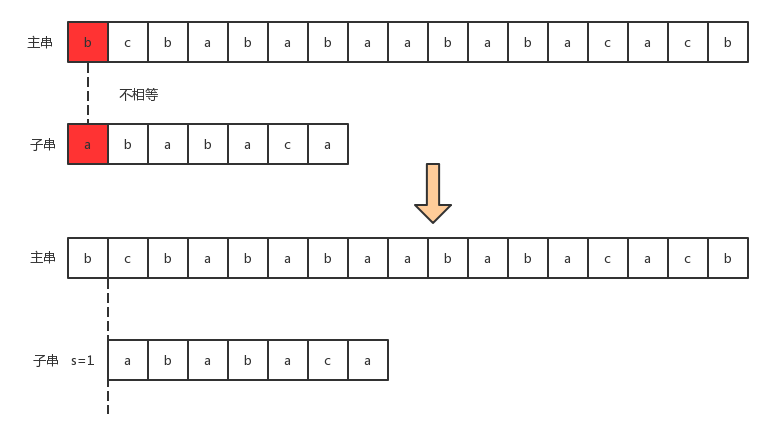
2）、依次对后面机会字符进行对比，直到s=3时，我们发现字符串 ababa 成功匹配，但是子串的第六个字符和主串的第九个字符并不相等：

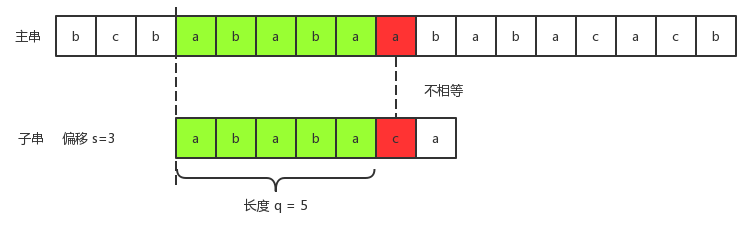
这时候失效函数就派上用途了。此时已匹配长度q=5，也就是说在状态转换图中对应于状态5。而状态5对应的失效函数值为3，对于串ababa来说，长度为3的串aba既是它的真前缀，又是它后缀的子串。此时主串和子串中的aba已经失效，已经没有再去比较的意义了，我们可以直接去比较主串中的a和子串中的b了：

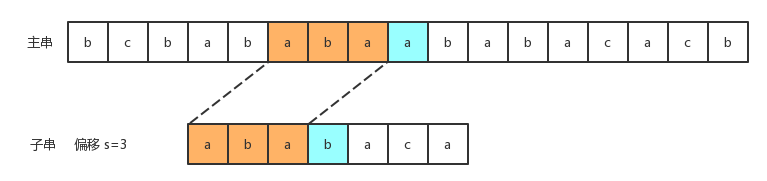
3）、现在我们将子串向右边移动2个字符，然后继续进行比较：

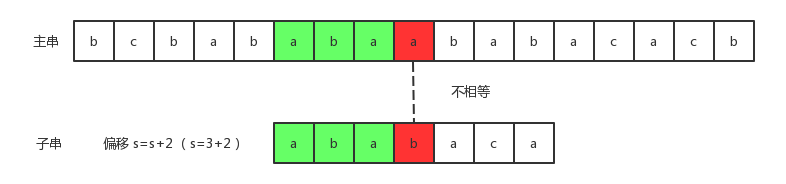
这里计算偏移量s很重要：

⚠️⚠️⚠️ s = s + (state - f(state))

比如这里的q=5，也就说明state=5，而f(state) = 3。因此向右的偏移量为：s = 3 + (5-3) = 5。

4）从图中标红也能看出来a≠b，因此我们需要继续重复步骤3的事情：

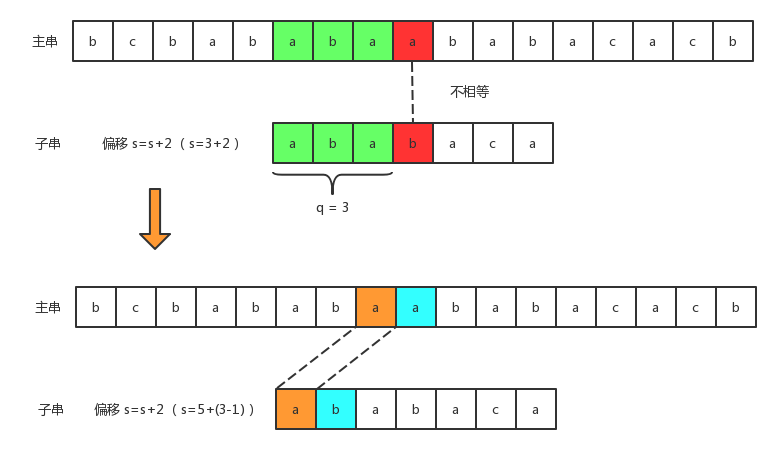
5）、如上图所示，我们继续将子串向右移动2个字符，进行比较：

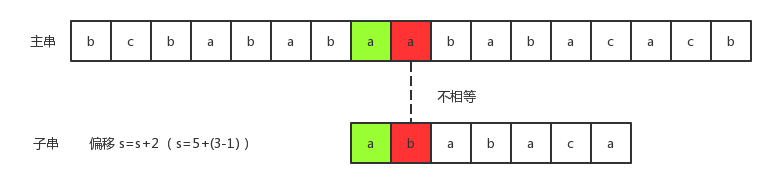
相等。但这里有一个需要注意的点是：此时state为1，而f(state)=0。这意味着此时并没有存在即是真前缀又是后缀的子串。
现在只能和第一步一样，手动将偏移量加1。

6）、现在将偏移量加1之后，并将子串和主串进行匹配。此时匹配成功，因为我们可以判断主串是包含有指定关键字的字符串：

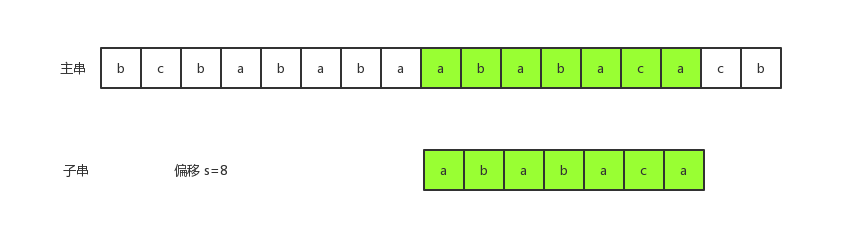
下面是简单的代码实现，需要注意的是这里并没有做极端情况的处理：

int kmp_match(string text, string pattern) {
	vector<int> trie(pattern.size() + 1);
	trie_func(pattern, trie);
	int offset = -1;
	int q = 0;
	string::size_type m = text.size();
	string::size_type n = pattern.size();
	if (m < n)
	{
		return -1;
	}
	for (string::size_type i = 0; i < m; i++)
	{
		while (q > 0 && text[i] != pattern[q] && q != 0)
		{
			q = trie[q];
		}
		if (text[i] == pattern[q])
		{
			q++;
		}
		if (q==n)
		{
			offset = i - q + 1;
		}
	}
	return offset;
}
int main()
{
	string text("bcbababaababacacd");
	string pattern("ababaca");
	int offset = kmp_match(text, pattern);
	cout << "offset: " << offset << endl;
}

总结

本节到这儿，我们已经能够手工地为各类词法单元构造状态转换图了。这类词法单元包括有：标识符（包括字符）、数字（包括数位）、关键字、运算符等等，而且也知道如何使用KMP算法来寻找指定串，例如标识符和关键字等等。
在下一节就需要通过自动地方式里生层对应的状态图了。