在上篇文章中，我们至少学会了将正则表达式构造成对应的NFA和DFA。但是用上篇文章中从正则表达式转换为对应DFA的方式效率低下，即我们要先将正则表达式转换为NFA，然后使用子集构造法将NFA转换为对应DFA。

在本篇文章中，我们将首先学习如何将正则表达式直接转换为DFA，并最小化DFA的状态数目。然后看看DFA模拟中时间和空间的权衡问题。

在正式进入正则表达式转换为DFA之前我们需要一些基本概念，没有这些基本概念可能不太好理解后面提到的内容。

一、需要的基本概念

重要状态

NFA的重要状态直接对应于正则表达式中存放字母表中符号的位置，而 重要状态是指NFA的某一状态有一个标号为非空的离开转换 。比如我们在上一节中将正则表达式转换为对应NFA时引入了新状态，它们的离开转换都是空转换，因此它们并不是重要状态。

每个重要状态对应于正则表达式中某个运算分量 。

因此我们在比较两个NFA状态集合时，判断它们是否一致的依据如下：
1）、具有相同的重要状态；
2）、要么都包含接受状态，要么都不包含接受状态；

抽象语法树

注意这里的抽象语法树和上一节提到的语法分析树有一点不同，关于语法分析树可以回去看上一篇提到的语法分析树定义。但抽象语法树是必须要完全理解的。

抽象语法树中，每个内部结点代表一个运算符，该运算符结点的子结点代表这个运算符的运算分量 !!!

在抽象语法树中，内部结点代表的是程序的构造；而在语法分析树中，内部结点代表的是非终结符。有时候我们将语法分析树称为具体语法树；而抽象语法树简称为语法树。这是因为在文法的很多非终结符都代表程序的具体构造，还有各种辅助符号。而这些在抽象语法树中都是不需要的。

而前面提到的重要状态就是抽象语法树中运算符的运算分量。下面是正则表达式 (a|b)*abb对应的抽象语法树：

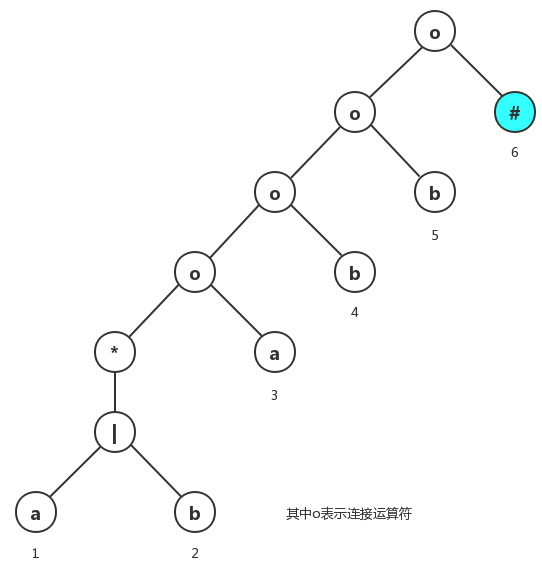
(a|b)*abb的抽象语法树

1）、结束标记符#：前面我们提到了重要状态，但（NFA或者DFA）接受状态没有一个标号为非空的离开转换，因此接受状态为非重要状态。基于此，我们可以给正则表达式的右边连接一个结束标记符 # ，使得正则表达式的接受状态成为重要状态。那么我们也就不用特殊处理接受状态了。

2）、叶子节点位置：上面抽象语法树叶子结点下方都有一个有序的整数，我们称这个整数为对应叶子的结点的位置。非空的叶子结点才会赋予相应的整数，也就是说为空串的叶子结点我们不需要对其增加位置。

二、nullable、firstpos、lastpos和followpos函数

我们要从一个正则表达式直接构造出DFA，除了前面我们已经构造了的抽象语法树之外，我们还需要计算nullable、firstpos、lastpos和followpos函数。

  • 1）、bool nullable(n)：其中n的取值为抽象语法树中任意结点（可以是叶子结点，也可以是是内部结点。即运算符和运算分量），其返回值的逻辑是当此结点的子表达式中包含有空串ε时返回true，否则为false；
  • 2）、nodes firstpos(n)：子表达式的语言中某个串的第一个符号，该语言是以n为根的子表达式；
  • 3）、nodes lastpos(n)：子表达式的语言中某个串的最后一个符号，同样的该语言也是以n为根的子表达式；
  • 4）、nodes followpos(n)：这相对要复杂一点。比如在抽象语法树中存在两个结点分别为n和m，存在某个串s = a1…aiai+1…ap，即以该正则表达式为模式的串。要满足followpos(n)==m，那么则需要ai和位置n匹配，aI+1和位置m匹配。比如当前有一个符号串aabb，想要构造该串对应于上图抽象语法树中各个节点顺序为1、3、4、5，因此我们就说follow(3)=4。通俗一点说就是要看抽象语法树指定结点的followpos，需要先找到对应结点在某个符号串中的位置，然后看该符号后一位符号即可。

上面的nodes表示的结点集合。前面说的结点均指的是抽象语法树中的重要位置。

更详细点，当我们计算上面抽象语法树位置1的followpos，即followpos(1)。那么我们通过抽象语法树来看，位置1之后经过并运算和闭包运算可以得到的子串有：

1
2
3
aa;/// 第一个a来自于位置1，第二个a来自于位置1。闭包运算循环了两次；
ab;/// a来自于位置1，b来自于位置2。闭包运算循环了2次；
aa;///第一个a来自于位置1，第二个a来自于位置3。闭包运算循环了1次；

因此得到 followpos(1) = {1,2,3};

下表整理了计算nullable、firstpos、lastpos的计算规则：

序号 结点n nullabl(n) firstpos(n) lastpos(n)
1 标号为ε的叶子结点 true ∅ ∅
2 位置为i的叶子结点 false {i} {i}
3 并 结点n=c1,c2 nullable(c1) 逻辑或 nullable(c2) firstpos(c1) ∪ firstpos(c2) lastpos(c1) ∪ lastpos(c2)
4 连接 结点n=c1c2 nullable(c1) 逻辑与 nullable(c2) 如果 nullable(c1) 为真，那么值为firstpos(c1) ∪ firstpos(c2)。否则为firstpos(c1) 如果 nullable(c2) 为真，那么值为lastpos(c1) ∪ lastpos(c2)。否则为lastpos(c2)
5 闭包 结点n=c1* true firstpos(c1) lastpos(c1)

由于md格式问题，上表第3行的逗号“,”替换为正则表达式中的”|”符号。

  • 1、每个叶子结点的firstpos和lastpos只包含它自身。上表中第2点；
  • 2、“并” 结点的firstpos和lastpos分别是它所有子节点的firstpos和lastpos的并集。上表第3点；
  • 3、“闭包”结点的firstpos和lastpos分别是它唯一子节点的firstpos和lastpos。上表的第5点；
  • 4、对于“连接”结点而言，firstpos主要是看左子结点是否为空。而lastpos右子节点是否为空。

现在我们运用上面的规则，将第一节的抽象语法树中每个结点的firstpos和lastpos求出来。如下图：

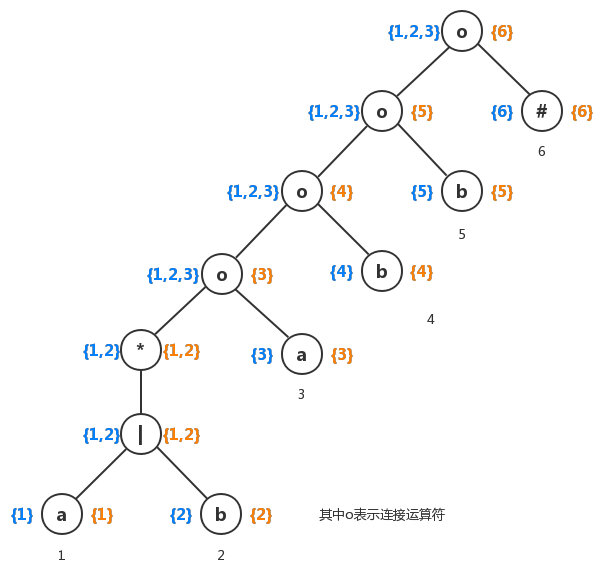
图中蓝色表示firstpos集合，而橙色表示lastpos集合。

计算followpos

只有两种情况会使得正则表达式的某个位置跟在另一个位置之后：

  • 1）、如果是结点n是一个“连接”结点，且在抽象语法树中其左右子节点分别为c1，c2。那么对于lastpos(c1)中的每个位置i，firstpos(c2)中所有位置都在followpos(i)中；
    通俗的讲就是以“连接”结点为根的子树，左子结点lastpos集合中每个位置的followpos都包含右子结点的firstpos。有点类似于二叉树后序遍历，左子树最大结点的后面跟着的是右子树的最小结点。

  • 2）、如果n是“闭包”结点，lastpos(n)中每个位置的followpos都包含于的firstpos(n)中；

基于上诉两个规则，我们对上面的图求解各个重要结点的followpos（上图已经标出每个结点的firstpos和lastpos）。下面是详细步骤：

  • 1、首先我们运用规则1来查看第一个“连接”结点，其左子结点的lastpos为{1,2}，并且其右子结点的firstpos为{3}。因此位置1结点和位置2结点的followpos都包含有位置3。

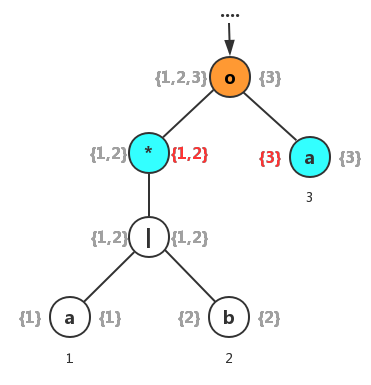
需要注意一点的是并不是看的当前结点本身的lastpos和firstpos，而是看的其左子结点的lastpos和右子结点的firstpos。

位置n followpos(n)
1 {3}
2 {3}
  • 2、同理我们将剩下的“连接”结点运用规则1，得到如下结果（这里太简单了我就不画图了）：
位置n followpos(n)
3 {4}
4 {5}
5 {6}
  • 3、现在是时候运用上面的规则2了，查找抽象语法树中的“闭包”结点。它和“连接”结点不同的是：“连接”结点看的是其左右子树的lastpos和firstpos，而“闭包”结点看的是其本身的lastpos和firstpos。

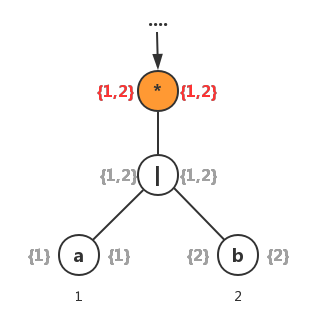
位置n followpos(n)
1 {1,2}
2 {1,2}
  • 4、现在我们将前面三步得到的数据进行合并之后的结果为：

很明显位置6作为增广正则表达式中存在的终结符标识，因此其followpos为空集。

位置n followpos(n)
1 {1,2,3}
2 {1,2,3}
3 {4}
4 {5}
5 {6}
6 ∅

回过头来看一下正则表表达式 (a|b)*abb匹配子串中，位置1对应的结点a其后可能存在字符为a（位置1）、b（位置2）、a（位置3）。位置2和位置1同理。

现在我们将每个位置，已经对应的followpos用一个有向图来表示如下：

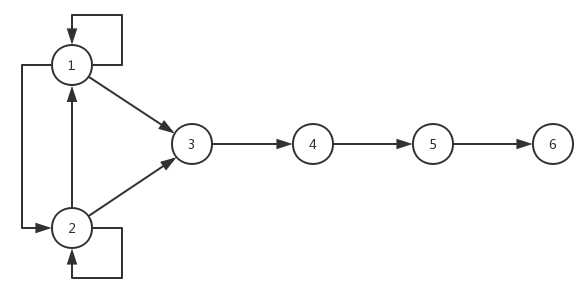
很明显的可以看出来，表示followpos函数的有向图几乎就是相应的正则表达式不包含空转换的NFA。

三、根据正则表达式构建DFA

要从一个正则表达式构造一个DFA的大致步骤如下：

  • 1、根据扩展的正则表达式构造出一个抽象语法树；
  • 2、计算每个节点的nullable函数值、firstpos函数值、lastpos函数值。以及重要位置节点的followpos函数值；
  • 3、抽象语法树根节点的 firstpos 作为DFA的开始状态；
  • 4、查看正则表达式中存在的各个转换（即a或者b），将当前状态中相同转换的followpos合并到一个集合中；
  • 5、如果合并的集合出现新的状态，则将该状态添加到DFA的状态集合中；
  • 6、如果经过各个转换之后没有新状态就停止。否则重复执行4~6步；

看一下例子能够更加清晰地认识到如何根据正则表达式构建DFA。

图中蓝色表示firstpos集合，而橙色表示lastpos集合。

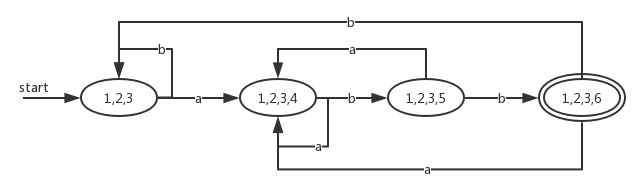
1）、对于正则表达式 (a|b)*abb，我们构造得到的抽象语法树，已经对应的firstpos/lastpos都在上图中;

2）、我们将根节点的firstpos = {1,2,3} 作为DFA的开始状态：

3）、该正则表达式中存在的转换有a, b，开始状态集合为{1,2,3}，此时我们将状态集合{1,2,3}相同状态的followpos合并到一个集合中。
集合{1,2,3}中对应转换a的位置有1，3；对应转换b的位置有{2}。
转换a的 followpos(1)={1,2,3}, followpos(3)={4}，将两个集合合并起来为 {1,2,3,4}，由于该状态是新状态，因此将状态集合{1,2,3,4}添加到DFA中；
转换b的followpos(2)={1,2,3}，由于该状态并不是新状态。因此只是一个简单转换即可。

重复执行第三步，得到的最终结果为：

基于抽象语法树得到的DFA

四、最小化DFA的状态数

对于同一个语言，可以存在多个识别此语言的DFA。例如上图和上一节中由NFA通过子集构造法得到的DFA都能够识别正则表达式 (a|b)*abb。可以看出来它们的个数也不一样。因此如果让我们使用DFA来实现词法分析器，我们肯定是希望使用状态数量尽量少的DFA了。

首先我们先看看区分状态的概念： 区分状态，如果从状态s和t出发，沿着标号为x的路径到达的两个状态中只有一个是接受状态，那么我们就说串x区分状态s和t。状态s和t是可区分的。
空串ε可以区分任何一个接受状态和非接受状态。

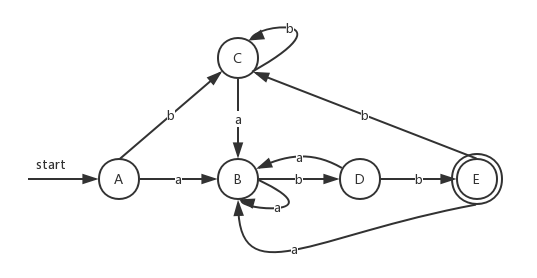
子集构造法得到的DFA

上图中串 bb 可以区分状态A和B，这是因为从A出发经过标号为bb的路径到达会接受状态C，而状态B经过标号bb的路径到达状态E接受状态。

其次还有一个重要的结论：任何正则语言都有一个唯一的状态数目最少的DFA。而且从任意一个接受相同语言的DFA出发，通过 分组、合并等价的状态，我们总是可以构建得到这个状态数量最少的DFA。

因此DFA状态最小化算法的工作原理是：

将一个DFA的状态集合划分成多个组，每个组中的各个状态之间相互不可区分，但是来自不同组任意的两个状态是可区分的（前面提到的区分概念）。

然后将每个组中的状态合并成状态最少DFA的一个状态。

最初，划分两个组：接受状态组和非接受状态组。基本步骤是从当前划分中取一个状态组，比如 A = {s1, s2, … , sk}，并选定某个输入符号a，检查a是否可以用于区分A组中的某些状态。查看s1, s2, … , sk在a上的转换，如果这些转换的到达的状态落入当前划分的两个或多个组中，我们就将A分割成多个组。

我们以上图为例来看看DFA状态最小化算法：
1）、首先划分两组：接受状态组合非接受状态组，这里我们分别给他们起名为组1和组2。

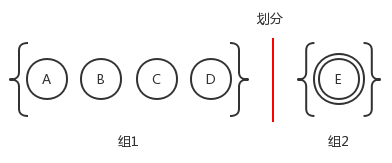
2）、在上图看到DFA仅有a、b两种转换。由于组2只包含了一个状态，并且该状态为接受状态而不能再被分割，所以组2原封不动。因此我们继续看组1。
组1中的状态A、B、C、D针对a的转换，得到的状态均为状态B，因此串a无法区分状态A、B、C、D。

3）、组1中的状态A、B、C、D针对b的转换，状态A、B、C都是到达组内某个成员上，这显然是无法区分的（前面提到过组内各个状态之间互不可区分）。但状态D到达的是组2成员对应的状态，很明显状态D可以和A、B、C区分开来。因此我们可以继续将组1划分更小的组：

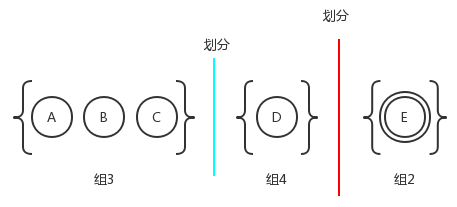
4）、类似于第三步，组3的状态A、B、C针对b的转换可以划分为两个不同的组。这是因为状态A、C经过转换b之后均为组内状态；而状态B经过转换b得到的组4成员对应的状态：

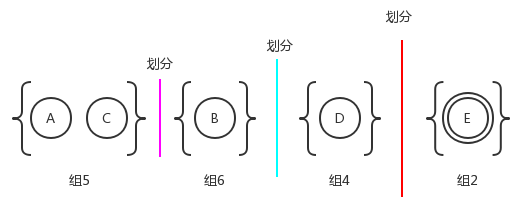
由于组5中各个状态，无论是针对转换a，还是转换b而言，得到的状态均相同。因此我们不能讲组5进行更细粒度的划分。那么上图就是最终的划分结果。

现在我们根据上面的信息画出对应的状态转换表，由于状态A和状态C经过转换得到的状态是一样的，因此集合{A,C}这里以状态A表示：

状态 a b
A B A
B B D
D B E
E B A

我们画出对应的DFA，并将其与上面我们用抽象语法树构造得到的DFA进行对比：

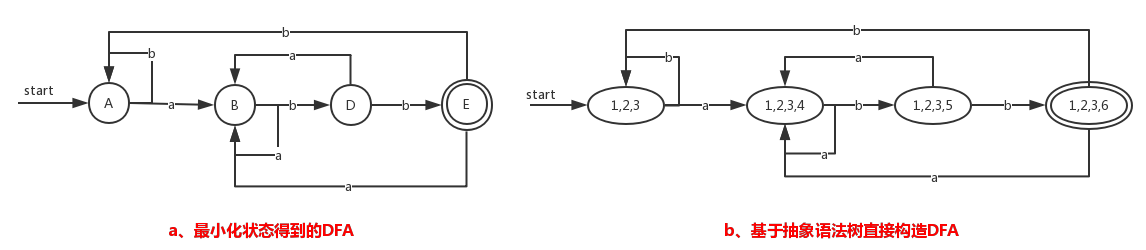
很明显能够对比出来，上面两个DFA除了赋予各个状态的名称不一样之外，各个转换以及转换后的状态都是一样的。我们称这两个状态机是同构的。同构是指对于两个不同的自动机，如果某个自动只是通过更改状态的名字就可以转换为另一个自动机。

五、DFA模拟中的时间和空间的权衡

最简单和最快捷的表示一个DFA的转换函数的方法是：使用一个以状态和字符为下标的二维表。给定一个状态和下一个输入字符，我们访问这个数组就可以找出下一个状态以及我们必须要执行的特殊动作。
但是我们知道对于二维表而言，各个状态针对某些字符并没有对应转换。如果数量变多了之后就会存在大量的空间浪费问题。

我们可以使用一个带有四个数组的数据结构，如下图所示：

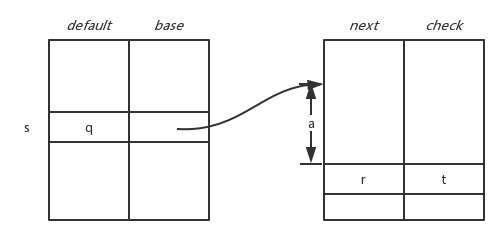
1）、base数组用于确定状态s条目的基准位置；
2）、next和check数组存放的正式对应状态条目；
3）、数组check用于确定base[s]给出的基准位置是否正确，如果错误则使用default数组来确定另一个基准位置；

在计算状态s在输入a的后继状态时，我们首先查看数组next和check中在位置 index = base[s] + a （a指当前输入字符，其对应于ascii码表上固定数字）上的状态条目。
a、如果check[index] == s，那么该状态条目有效（该状态指的是经过转换a之后得到的后续状态）；
b、如果check[index] != s，那我们则得到另一个状态条目t = default[s]。并将状态t设置为当前状态重复上诉过程获取下一个状态；

下面是对应的伪代码：

1
2
3
4
int nextState(s,a) {
  if(check[base[s]+a] == s) return next[base[s]+a];
  else return nextState(default[s],a);
}

总结

在这一节中需要重点理解的就是抽象语法树：抽象语法树的每个内部结点代表一个运算符，该内部结点的子节点代表运算符的运算分量。然后可以根据正则表达式构造对应的抽象语法树。
函数nullable、firspos、lastpos以及followpos在构造DFA中起着重要的作用。nullable指的是对应结点的子表达式是否可能返回空串；firstpos是子表表达式串的第一个符号；lastpos是子表达式串的最后一个符号；followpos则是相对要复杂一点，只针对连接结点和闭包结点求followpos。
在有了上面只是作为铺垫之后，求正则表达式来DFA的转换就要轻松许多。首先是在抽象语法树中以根节点所在的firstpos集合作为DFA的开始状态。然后查看集合内部各个序号对应的转换，获取对应需要的followpos求并集。以此类推下去可构造一个完整的DFA。
而在最小化DFA状态数时，则根据不同的划分，递归地将各组区分开来，得到状态数最少的DFA。而在最后也给出了权衡时间和空间的数据结构。

到这儿基本上把词法分析相关的知识都简单过了一遍了。后续再继续更新语法分析部分。