A Malloc Tutorial

前言

本篇文章是对该文章的翻译，如有疑问可对照原文。

一、介绍

什么是malloc？如果连这个名儿都没有听说的话，那么应该在读这篇文章之前先去学习一下Unix环境下的C语言。对于程序员来说，malloc是在C语言编程中分配一块内存的函数，然后大多数人并不知道其背后的真实情况，或者仅仅是认为这是一个syscall或者语言关键字。这篇文章中只需要一些C的技能和一些系统知识，就能了解到malloc也只不过是一个简单的函数而已。
本文的主要目的是编写一个简单的malloc函数，来帮助我们了解底层概念。其目的并不是为了实现一个高效的malloc，仅仅提供基础功能。但是背后的概念能够帮助我们有效地去理解进程中内存是如何管理的，以及如何处理块的分配，再分配以及释放等等。
站在教学的角度来说，这是一个很好的C语言编程练习。同样也是一个很好文档，它能够帮助我们理解指针怎么来的，它们在堆里面是怎样组织起来的。

malloc是什么

#include <stdlib.h>
 void *malloc(size_t size);

malloc是一个标准C库函数，用于分配内存块。它遵循以下规则：

• malloc至少要分配请求字节大小（size）内存；
• malloc的返回的指针，指向一个已分配的内存（比如一个在编程时可读或者可写的空间）；
• 在该指针没有被释放之前，其他任何的malloc调用都不会分配该空间或者该空间中的任何一部分；
• malloc应该能很好处理，而且能够很快执行结束；
• malloc需要提供重新设置大小或者释放的能力；

malloc函数返回的指针在失败或者没有可用内存空间的情况下为NULL。

二、堆和brk、sbrk系统调用

在编写malloc之前，我们需要理解内存在多任务系统中是如何管理的。由于具体实现依赖于操作系统的实现细节，下面提到的内容更多是基于抽象的概念来进行阐述。

进程的内存

每个进程都有它自己的虚拟地址空间，由MMU（内核）提供从虚拟地址空间到物理地址空间的转换。而该空间被分为多个部分，比如用户存储局部变量和volatile变量的栈，还有存储常量和全局变量的空间，以及用于存储程序数据，称为堆的散乱空间。

就虚拟地址而言，堆是一个连续的内存空间，它有三个划分的边界：起始点、最大值和称一个为break的终点。
最大值的管理可以调用(原文中写成了sys/ressource.h)里面的setrlimit和getrlimit。break用于标记已映射内存空间的尾部，已映射内存空间指的是已经和实际内存一一对应起来的那部分虚拟地址空间（我的理解也就是对应的PTE里面有效位应该是为1，更或者TLB有对应的缓存的Page）。下图展示了内存组织的形式：

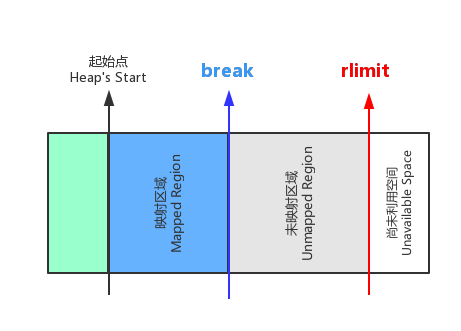
为了能够编写malloc函数，我们需要知道堆（heap）的开始位置和break的位置。当然我们还需要有能力去移动break，可以使用brk和sbrk系统调用来实现。

brk和sbrk

我们可以在他们的手册（比如man brk）里面找到关于这些系统调用的描述：

int brk(const void *addr);
void *sbrk(int incr);

brk函数通过传入的 addr 来设置brak的值，成功返回0，失败返回-1。使用全局errno来指明错误的原因（错误码对应的错误信息可以在\中查看）；

而sbrk通过传入的增量（以字节为单位）来移动break的位置。基于不同系统的实现，其返回值可能会返回老的地址，也可能返回移动之后新的地址。
如果函数调用失败则返回-1，并且设置errno的值。在有些系统上sbrk支持传入一个负数用于释放那些已被映射的地址空间。

由于sbrk没有规范其返回值的意义，因此我们在 移动break的时候 不会去使用它返回值。但是我们可以使用特定情况下的sbrk，当调用sbrk其增量为0时，它的返回值就是实际的break地址（也就是老的地址和新的地址是同一个值）。因此sbrk用于获取堆的开始位置，也就是break的初始位置（上图中mapped Region长度为0的时候，也就是break的初始位置）。

因此我们将使用sbrk作为我们主要的工具。而我们的目的是在需要更多空间的情况下，我们要做的就是获取更多的资源来满足需求。

未映射区域和无人区（No-Man’s Land）

我们看一下早期break标记已映射虚拟地址空间结束点的原理：在访问break之前的区域时会触发一个总线错误。在break点和最大限制（rlimit）之间的空间，系统（MMU和内核部分）是没有将物理内存和虚拟内存关联起来的。
如果知道一点关于虚拟内存的知识的话，应该清楚内存是通过页的方式来进行管理：物理内存和虚拟内存通常情况下以固定大小的页面进行组织，而页的大小在实际系统中通常为4096Byte（4KB）。因此break点可能并不是在整页的边界上。
说点题外话，在《现代操作系统》中介绍缺页处理程序是通过懒加载的方式来将物理内存和虚拟内存联系起来的。不考虑TLB的情况下，MMU是将VPN和PPN通过PTE来进行映射的

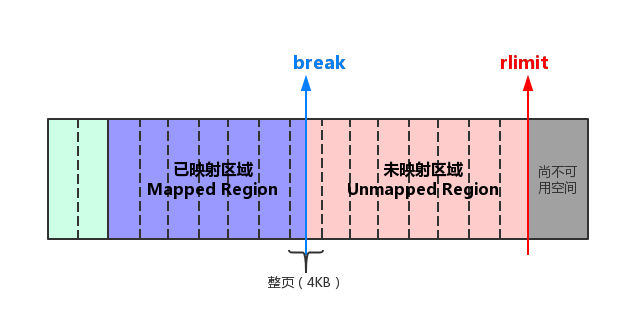
图二相比于图一，我们增加了页面边界的表示。可以看到break并没有和页边界吻合对应起来。那么处于break和下一页边界之间的内存是什么状态呢？实际上，这一段空间是可用的，我们可以对这段空间进行读写操作。但问题在于我们没有办法知道下一页边界的任何头绪，它的实现是非常依赖于特定系统的，所以对于可移植性来说，不建议这么去做。

无人区（no-man’s land）可能是大部分BUG的根源：在堆外面进行错误地指针操作时，对于小规模测试大部分时间是可以成功的，但是在更大量数据的时候该操作就会出现失败。

mmap

尽管在这个教程中我们并不会使用它，但是我们应该要注意到mmap系统调用。mmap大部分情况用于将文件和内存映射起来，但是它可以以匿名模式来实现malloc（在某些特定情况下）。
匿名模式下的mmap可以分配指定数量的内存（以页面大小为单位），munmap可以释放掉它们。使用这种方式实现的malloc相较于传统基于sbrk实现的malloc通过更加简单。 有些malloc使用mmap来实现大内存的分配（超过一页的大小）。
OpenBSD的做法是使用mmap并搭配一些奇技淫巧来增加安全性（页与页之间在分配的时候增加边框来进行分配。这里翻译不太顺，加边框的意思是在页的边界处使用额外的空间来达到整页使用的效果，想象卷积的时候增加padding来读取矩阵左上角的数据。如果翻译有问题请联系我）。

三、Dummy malloc

首先，我们会使用sbrk来假设一个malloc。这个版本的malloc可能是最差的一个，甚至是最简单的一个。

原理

思想很简单，每次在调用malloc的时候，我们根据请求的空间大小来移动break，并且返回break之前的地址。这样做的确够简单，也够快。。。它仅仅只需要三行代码。但是这样的话我们没法去实现一个真实的free，当然realloc同样也不行。

这个版本的malloc会浪费很大一部分用过的内存块儿。在这儿只是出于科普的目的来指出如何sbrk系统调用，同样还将为malloc添加一些错误管理。

实现

void *malloc(size_t size){
    void *p;
    p = sbrk(0);
    /// 如果sbrk失败，返回NULL
    if (-1 == sbrk(size)) {
        return NULL;
    }
    return p;
}

四、组织堆（Organizing the Heap）

在上一节我们写了第一个版本的malloc函数，但是并没有满足我们所有的需求（前面提到的free和realloc）。在这一节我们会尝试找到一个高效组织heap的方案，其中包括了malloc、free和realloc。

我们需要什么

如果我们在编程上下文之外思考问题，能推断出在解决这个问题的时候我们需要哪些信息吗？来看个比喻：你拥有一片农场，并将他们划分成很多块农田区域出来。将这些分块的农田出租出去。租户希望租用连续的，但不同长度的农田（这里只使用长度这个维度来划分，不考虑面积）。当租户使用完成之后将其租用农田归还，以便下次继续向外出租。

在农场边提供了用于行驶“可编程”车的道路：输入距离开始点的偏移量和目的地（目的地是一块不是一个点，所以这里表达的是该块的开始点位）。因此我们需要知道每一块的开始点在哪儿，而且当我们处于某一块的起始点的时候，我们还需要知道下一块的地址。

其中一个解决方案是在每一块农田的开头部分放入一个标签来标明下一块的地址（和当前块的大小以避免不必要的计算），当租户将农田资源归还的时候，在空闲区域添加一个标记。
好了，现在当租户想要固定大小农田的时候，我们可以带着他行驶在一处一处的标签那儿去。当我们发现一块标记为可用状态的农田，并且足够交付租户需求的时候，我们将该空闲标记从标签中移除。但是如果到达最后一块农田（也就是标签中没有下一个农田的地址），我们只需要到达该区域的末尾并添加一个新的标记。

现在我们将这个比喻转换到内存： 我们需要在每一块开始部分存储额外的信息，包括每一个块的大小、下一个块的地址、以及是否空闲等信息。

如何表示块信息

我们需要在每一个大块（chunk）的开始部分包含一小段（block）用于容纳额外信息，这一小段我们成为“meta-data”；该段至少包含了下一块的指针、用于空闲块的标记、以及该块数据大小。当然，该段信息是在mallc函数返回的指针之前。

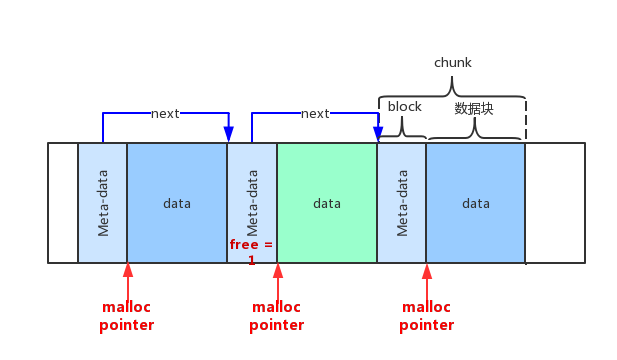
图三展示了一个堆组织的例子，含有已分配段前面的meta-data。 每一个大块（chunk）由数据块和meta-data组成，malloc函数返回的指针在上图下面由红色标记出来，需要注意的是该指针是指向的数据块，并不是完整的大块（chunk，不是指向meta-data的起始点）。
现在我们需要怎样来把这些用C代码表示出来呢？这个看起来像传统的链表（实际上就是个链表）。我们编写一个链表类型，该类型成员用来表示所需的信息。我们使用 typedef来简化结构类型：

typedef struct s_block* t_block;
struct s_block {
    size_t size;
    t_block next;
    int free;
};

在这儿看起来使用int型的free标记有点浪费空间，但由于struct默认是内存对齐的，因此它不会改变任何内容，稍后我们会看到如何缩小meta-data的大小。后续我们会看到malloc返回的地址必须是内存对齐的地址。
这儿出现最频繁的问题是：我们如何在没有malloc的情况下去创建一个struct？答案很简单，我们只需要知道struct实际上是什么。在内存中，struct只是将一块儿区域结合了起来，所以结构s_block仅仅只是12字节（对于32位整型来说）。size字段对应前面的4字节，接下来的4字节是指向下一个block的next指针，最后4个字节是一个整型的free标记。
当编译器遇到访问结构的域时（比如s.free或者p->free），将其转换为该结构的基地址加上该域之前长度的和。比如：p->free就是((char )p+8)，s.free就是((char )&s+8)。我们所需要做的就是使用sbrk分配足够的空间块（包含了meta-data的大小和数据块的大小），并将老的break放入t_block类型的变量内：

/* Example of using t_block without malloc */
t_block b;
/// 使用b保存老的break
b = sbrk(0);
/// 添加所需空间
/// size变量是malloc函数的参数
sbrk(sizeof(struct s_block)+size);
b->size = size;

五、首次适配策略的malloc

“首次适配”是我采用《深入了解计算计算机系统》的翻译词。在这一节我们将会实现经典的首次适配策略的malloc函数。首次适配算法很简单：我们只要找到了一个空间大小足够满足请求分配的时候就停止遍历其他的块（chunk）。

指针对齐

通常情况需要将指针和整型大小对齐（即 指针大小就是一个整型的大小）。此处我们只考虑32位的情况，所以指针是4的倍数（32bit = 4 byte，那当然是4的倍数）。因此我们的meta-data已对齐，我们仅仅需要做的只是去对齐数据块的大小。
那我们该怎么做呢？这儿有几种方式，最有效的方式是使用算术技巧添加预处理宏。
首先，算术技巧：给定任意正整数除以4，然后再将它乘以4得到最接近4的倍数。因此为了获得最接近且大于它时，只需要乘以4，然后在此基础上加4。这种方式的确很简单，但它没办法很好地工作在本身就是4的倍数上，结果会变成4的倍数的下一个（由于加了4）。
再来使用一次算术，假设x是整型，并且满足：

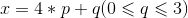
1）、如果x是4的倍数，那么q = 0，并且满足：

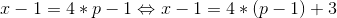
运用上面说的，先除以4，然后乘以4，最后再加上4：

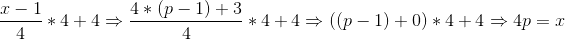
在这个推算过程是将上面x-1的表示用p来进行表示。这里需要注意一点的是，在整型除法中3/4结果为0；

2）、如果x不是4的倍数，此时q != 0：

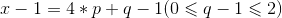
同样运用上面的，先除以4，然后乘以4，最后再加上4：

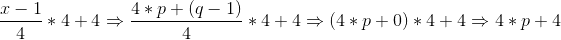
因此，公式 _(x-1)/4 * 4 + 4_ 的结果是最接近并且大于或者等于4的倍数。

那么我们在C里面该怎么做呢？首先，注意到除法和乘法我们可以使用右移和左移移位操作符来解决（>>和<<），它们相对于简单乘法要快很多。因此我们的公式在C里面可以写成这样 ((x-1)>>2)<<2+4，但是在宏里面需要使用额外的括号：

#define align4(x) (((((x)-1)>>2)<<2)+4)

寻找块：首次适配算法

找到一个足够长度的块非常简单：从堆的起始点开始（以某种方式会保存在代码，后续会看到）测试当前块，如果该块成功适配则返回该块的头部，否则继续向下一块寻找，直到最后一个块的头部。
这里唯一的技巧是需要保存上一次遍历过的块，所以当没有找到合适的块的时候，malloc函数可以很轻松地去扩展堆的尾部（长度）。代码逻辑很直接，base是一个全局指针变量，指向堆的开始位置：

t_block find_block(t_block *last, size_t size) {
    t_block b = base;
    while (b && !(b->free && b->size >= size)) {
        *last = b;
        b = b->next;
    }
    return b;
}

这个函数会返回一个合适的块，或者返回NULL（在没有找到的情况下）。函数执行后，last指针指向上一次访问过的块。

扩展堆

现在，并不能总是找到合适的块，有时候（特别是最开始使用malloc函数）需要去扩展堆。
实现同样很简单：移动break，并初始化新的block。当然还需要更新堆中上一个块的next域。
在后续开发过程中需要知道struct s_block的大小，所以在这儿定义一个宏：

#define BLOCK_SZIE sizeof(struct s_block)

下面代码没有什么可惊讶的，仅仅只是当sbrk失败之后返回NULL（没必要想这么做的原因）。
注意，前面提到过我们不能确信sbrk函数返回的上一个break，因此我们首先保存break值，然后移动它。我们需要使用last和last->size来进行计算：

t_block extend_heap(t_block last, size_t size){
    t_block b;
    b = sbrk(0);
    if ((void *)-1 == sbrk(BLOCK_SZIE+size)) {
        /// sbrk失败
        return NULL;
    }
    b->size = size;
    b->next = NULL;
    if (last) {
        last->next = b;
    }
    b->free = 0;
    return b;
}

拆分块（block）

注意到我们寻找首个可用的块，但并没有管它的大小（足够大）。假想一下，如果只需要2byte的大小，但是找到的块是256byte的，如果这样做会丢失很大一部分的空间。第一个解决方案是拆分块：当一个块足够宽到请求的大小加上一个新块大小（至少BLOCK_SIZE+4），那么向链表中插入一个新块。

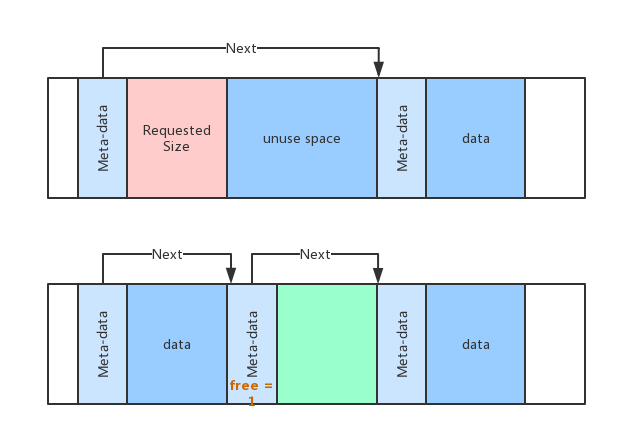
下面的函数（split_block）会在空间可用的时候被调用。提供的大小(参数size)必须要是对齐的。
在这个函数中我们会做一些关于指针运算，为了防止错误，我们将使用一些小技巧来确保我们所有的操作都以一个字节的精度完成（需要注意一下p+1是依赖于p的类型的，也就是不同类型指针加一的步长不一样）。
我们只需要在struct s_block中添加一个字符数组的域。结构体中添加数组很简单：数组直接定义在结构的内存块中，因此数组指针的作用是指向meta-data的尾部。C禁止长度为零的数组，那么我们就定义个一字节长的数组：

struct s_block {
	size_t size;
	t_block next;
	int free;
	char data[1];
};

并且需要更新一下宏BLOCK_SIZE的值，由于扩展了s_block的data，如果还是使用sizeof的话将会把data字段也算进去。所以这里需要将BLOCK_SIZE固定位12字节（注意，现在说的32位整型）：

#define BLOCK_SZIE 12

这里我说一下这里加了一个data域，为什么BLOCK_SIZE要设置为12，不随sizeof(struct s_block)呢？
前面也说过结构只是把内存里面的各个字节赋予了含义而已，我们只是想把12字节认为是meta-data，而并不是硬生生得塞了一块数据到meta-data和数据块之间。
加这个域只是为了我们在拆分block的时候方便，不加这个域同样也是可以操作的。

增加了这个扩展之后，并不需要明确为之前 extend_heap函数适配新增的data域。函数split_block：会根据传入的参数来拆分为所需大小的块。图四展示该函数的相关操作：

/// 参数s必须要对齐的
void split_block(t_block b, size_t s) {
    if (!b) {
        return;
    }
    t_block new;
    new = b->data + s;
    new->size = b->size - s - BLOCK_SZIE;
    new->free = 1;
    new->next = b->next;
    
    b->size = s;
    b->next = new;
}

注意代码b->data+s，由于data域时char[]类型，所以我们能够精确地控制是以字节的步长进行增加。

malloc函数

现在我们可以开始写malloc函数了，它主要是将前面讲到的函数封装起来。我们必须要将请求的size对齐，并测试是否是第一次调用malloc函数，以及已告知其余所需的条件。
在上一节的find_block函数中使用了一个全局变量 base，下面是该变量的定义：

void *base = NULL;

它是一个void *类型的指针，并初始化为NULL。在malloc中我们首先要做的就是判断base是否为NULL？如果为NULL那么就表示第一次调用malloc函数，否则就是用前面提到的相关算法。

malloc函数需要具备下面几行中的特性：

• 首先需要对齐请求的大小；
• 当base已经初始化：
  • 搜索足够大小的空闲块；
  • 如果找到该块的情况下：
    • 尝试着去拆分该块（请求的大小和块的大小足够存储meta-data和最小块数据，比如4byte）；
    • 标记该块为已是用(b->free = 0)；
  • 否则：扩展堆；注意在find_block函数中使用的last指针，它用于记录上一次访问过的块（chunk），因此当我们在扩展块的时候就不用再重新去遍历整个链表。
• 否则：扩展堆（空指针）。注意此时工作在extend_heap函数时last=NULL。

也需要注意在每次失败之后，我们按照预期指定的malloc函数返回NULL。

void *malloc(size_t size){
    t_block last,b;
    size_t align_size = align4(size);
    if (base) {
        last = base;
        if ((b = find_block(&last, align_size))) {
            if (b->size - align_size >= (BLOCK_SZIE + 4)) {/// meta-data + 4
                split_block(b, align_size);
            }
            b->free = 0;
        }else{///查找heap失败，extend heap
            b = extend_heap(base, align_size);
            if (!b) {
                return NULL;
            }
        }
    }else{///首次调用malloc函数，extend heap
        /// base = null;
        b = extend_heap(base, align_size);
        if (!b) {
            return NULL;
        }
        base = b;
    }
    return b->data;
}

六、calloc, free和realloc函数

calloc函数

calloc函数：

• 首先调用malloc函数，并分配正确的大小；
• 将块里面的每一个字节设置为0；

这里使用一个小技巧：chunk中数据块的大小总是4的倍数，所以我们以4字节的步长进行迭代。因此我们把new指针当做无符号整型的数组：

void *calloc(size_t number, size_t size) {
    size_t *new;
    size_t s4,i;
    new = malloc(number*size);
    if (new) {
        s4 = align4(number*size)<<2;
        for (i = 0; i < s4; i++) {
            new[i] = 0;/// new为size_t，所以这里+1的步长为size_t的字节数，在32位整型下面，size_t为4字节
        }
    }
    return 0;
}

free函数

注：在下文提到的块在原文中的描述如果没有特殊注明均为chunk，而非在malloc一节大量使用的block。

快速实现free是很简单的，但简单并不意味着很方便就能完成。我们有两个问题：找到被释放的块，并且防止出现空间碎片。

碎片：malloc函数遗留问题

malloc函数的一个重大问题是碎片：在多次使用malloc和free之后，堆被划分为许多块，这些块已经小到足够满足大的malloc，直到整个可用空间使用。这就是空间碎片的问题。在这个算法中我们虽然没有办法避免出现额外的碎片，但可以避免其他来源的碎片。
当我们选择的空闲块足以容纳请求分配的量和另外的块时，我们会拆分当前块。在提供更好地内存使用率（新的块为空闲状态以备后用）的同时也引入了更多的碎片。
解决碎片化的一个问题就是空闲块。当我们释放一个块时，如果临接的块同样是空闲状态时，我们合并他们成一个更大的块。在这儿我们所有需要的就是去测试前面块和后面块的状态。那么如何去获取之前的块（block）呢？下面有几个解决方案：

• 从头开始搜索，但非常慢（特别是我们已经搜了一些空闲块之后，再从头搜索）；
• 当我们搜索到当前块的时候，使用一个指针指向上一个访问的块；
• 双链表；

我们选择最后这个解决方案，该方案非常简单地去跟踪目标块。所以我们再一次去修改struct s_block（第一次修改是malloc的时候增加的data成员）。但由于我们还有另外一个待修改的地方（下一节），因此先不急着做修改。

所以我们现在要做的就是合并，我们先写一个简单的合并函数来合并块。在下面的代码中我们会用一个 prev域来作为直接前驱：

t_block fusion(t_block b) {
    if (b->next && b->next->free) {
        b->size += BLOCK_SZIE + b->next->size;
        b->next = b->next->next;
        if (b->next) {
            b->next->prev = b;
        }
    }
    return b;
}

fusion函数很直截了当：如果下一个块是空闲块，那么就将当前块的size和下一个块的size，以及meta-data的大小。然后将next域指向当前变量后继的后继（b->next->next），此时如果当前的后继存在，那么久更新该后继的直接前驱（b->next->prev）。

找到正确的块

关于其余释放带来的问题是如何高效地寻找由malloc函数返回的正确的块。实际上，这儿存在几个问题：

• 验证输入的指针（它是否真的是一个malloc指针）；
• 找到meta-data指针；

我们可以通过quick range test来消除无用的指针：如果该指针在堆外，那么它肯定不是一个有效指针。那么剩下的case和上一个case相关，我们如何确定该指针是由malloc函数获得？
其中一个解决方案是在结构内使用一个魔数（magic number）。相对于魔数更优的一个方案是我们可以使用一个指针指向它自己。解释一下：我们有一个ptr域指向data域，如果b->ptr == b->data的时候，那么该指针大概率是有效块（block）。
下面是扩展之后的结构，以及访问和校验给定的指针是否为相应的块（block）：

typedef struct s_block* t_block;
struct s_block {
    size_t size;
    t_block next;/// 后继
    t_block prev;/// 前驱
    int free;
    void *ptr;
    char data[1];
};

t_block get_block(void *p){
    char *tmp;
    tmp = p;
    tmp = tmp-BLOCK_SZIE;
    p = tmp;
    return p;
}

int vaild_addr(void *p) {
    if (base) {
        if (p > base && p < sbrk(0)) {/// sbrk(0)是获取当前break线，结合前面提到的图
            return p == (get_block(p)->ptr);
        }
    }
    return 0;
}

实现free函数

free函数到现在也渐渐揭开了神秘面纱：验证指针的正确性，并找到相应的块，然后将其标记为空闲块，最后如果有必要就进行合并操作。
释放内存时，当我们处于堆的尾部，我们需要调用一下brk函数来调整break先到当前块的位置处。
下面的代码展示具体实现，大致的逻辑如下：

• 如果指针有效：
  • 获取block块的地址；
  • 标记为空闲状态；
  • 如果当前节点的直接前驱是空闲的，那么就合并两个块；
  • 继续尝试合并直接后继块；
  • 如果当前处于最后一个块，那么我们释放内存；
  • 如果这儿没有更多的块了，那我们重置为原始状态（base设置为NULL）；
• 如果该指针不是有效指针的话，我们就什么也不做；

void free(void *ptr) {
    t_block b;
    if (vaild_addr(ptr)) {
        b = get_block(ptr);
        b->free = 1;
        /// 如果可以合并直接前驱
        if (b->prev && b->prev->free) {
            b = fusion(b->prev);
        }
        /// 合并直接后继
        if (b->next) {
            fusion(b);
        }else{
            if (b->prev) {
                b->prev->next = NULL;
            }else{
                base = NULL;
            }
            brk(0);
        }
    }
}

使用realloc重置块的大小

realloc函数和calloc函数差不多一样直接。基本上我们只需要一个内存拷贝的操作，在这里我们不使用里面的memcpy我们可以写一个更好的（大小以块为单位，并且已经对齐）。拷贝函数如下：

void copy_block(t_block src, t_block dst) {
    int *sdata;
    int *ddata;
    size_t i;
    sdata = src->ptr;
    ddata = dst->ptr;
    for (i = 0; src->size > 4*i && dst->size > 4*i; i++) {
        ddata[i] = sdata[i];
    }
}

按照下面的做法可以实现一个非常幼稚（但是能工作）的realloc函数：

• 使用malloc根据指定的大小分噢诶一个新块；
• 将数据从旧内存数据复制到新内存地址处；
• 释放旧内存中的数据；
• 返回指向内内存地址处的指针；

当然我们还想做一点事儿让realloc函数更高效一点。当我们有足够的空间的时候，此时并不需要去分配新的空间。因此不同点有：

• 如果大小未发生变化，或者额外可用大小足够使用，那么我们什么也不做；
• 如果需要收缩块，那么拆分该块；
• 如果下一个是空闲块而且提供了足够的空间，如果需要的话我们可以合并或者拆分这些块；

下面是realloc函数的具体实现：

void *realloc(void *p, size_t size) {
    if (NULL == p) {
        return malloc(size);
    }
    size_t s;
    t_block b, new;
    void *newp;
    if (vaild_addr(p)) {
        s = align4(size);
        b = get_block(p);
        if (b->size > s) {
            if (b->size >= s+BLOCK_SZIE+4) {
                split_block(b, s);
            }
        }else{
            if (b->next && b->next->free && (b->next->size + b->size + BLOCK_SZIE) >= s) {
                fusion(b);
                if (b->size - s > BLOCK_SZIE+4) {
                    split_block(b, s);
                }
            }else{
                newp = malloc(s);
                if (!newp) {
                    return NULL;
                }else{
                    new = get_block(newp);
                    copy_block(b, new);
                    free(p);
                    return newp;
                }
            }
        }
    }
    return p;
}

别忘了realloc(NULL, s)是可以直接提到malloc(s)的。

FreeBSD中reallocf函数

FreeBSD提供了另外一个realloc函数的实现：reallocf，它会在任何情况下释放输入的指针（即使是再分配失败之后）。我们一样会调用realloc函数，但是只有我们在获得空的指针之后才会调用free函数。下面是具体的实现部分：

void *reallocf(void *p, size_t size) {
    void *ptr = realloc(p, size);
    if (!p) {
        free(p);
    }
    return ptr;
}

到这儿基本翻译完成，如有错误请及时来联系我，谢谢❤️